Wie den Scheitelpunkt berechnen?
Ich frage mich wie man bei so einer Funktionsgleichung den Scheitelpunkt berechnen kann:
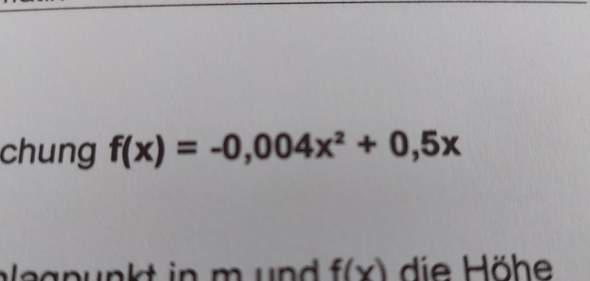
Ich kenne das nur an z.B: 0,09x² + 8x + 4. Da man an so einer Funktionsgleichung sehr gut die P/-Q Formel anwenden kann, oder sie in die Scheitelpunktform umwandeln kann.
Doch bei dieser Funktionsgleichung (-0,004x² + 0,5x) bin ich überfragt.
3 Antworten
ich kenne das nur an z.B: 0,09x² + 8x + 4.
Und warum klappt das jetzt bei nicht bei:
Was ist hier fundamental anders? Es sind lediglich andere Zahlenwerte.
Schneller geht es hier aber mit dem Satz vom Nullprodukt die Nullstellen zu bestimmen:
Hallo.
Dazu gibt es diverse Möglichkeiten. Zum Beispiel mittels quadratischer Ergänzung, PQ Formel, Ableitung, usw.
Bei dem Beispiel kannst du auch die von dir bevorzugte PQ Variante anwenden, wenn du das möchtest. Nur weil Q=0 ist, ändert sich ja nichts daran.
f(x) = -0,004x² + 0,5x
-(4/1000)x² + 1/2x = 0 | : -(4/1000)
x² - 125x = 0
Das -p/2 entspricht also 62,5. Das als x noch in die Funktion einsetzen für das y
y = -0,004*62,5² + 0,5*62,5
y = 15,625
SP(62,5|15,625)
..........................
Über die Ableitung:
f(x) = -0,004x² + 0,5x
f'(x) = -0,008x + 0,5
-0,008x + 0,5 = 0 | -0,5
-0,008x = -0,5 | : (-0,008)
x = 1000/16 = 500/8 = 250/4 = 125/2 = 62,5
Führt dich ebenfalls zum selben x.
..........................
Für die quadratische Ergänzung, guck mal hier vorbei
https://studyflix.de/mathematik/quadratische-ergaenzung-1897
Das ist eine Quadratische Funktion. Diese haben nur einen Extrempunkt, nämlich den Scheitelpunkt. Merk dir hierfür einfach die Formel
-b/2a („ minus b durch zwei a)
b= Zahl vor dem x
a= Zahl vor dem x^2.
Warum diese Formel gilt kannst du dir erschließen, sobald du über etwas über Ableitungen gelernt hast.