Mathe Funktion ausklammern was wurde hier gemacht?

-x³+3x+2

(x+1) (-x²+x+2)

-x²+x+2=0 | PQ

Ich verstehe hier nicht genau wie ausgeklammert wurde. (x+1) dann müsste doch die Funktion -x²+0+2= lauten und nicht +x+2?

Answer 1

[Caralina8]

Multiplizierst du die Klammern aus passiert folgendes:

(x+1) * -x^2 = -x^3 - x^2

(x+1) * x = x^2 + 1x

(x+1)*2 = 2x + 2

Zusammengefasst ergibt das:

-x^3 - x^2 + x^2 + 1x + 2x + 2

= -x^3 + 3x + 2

Es entspricht also dem Ausgangsterm.

Answer 2

[Halbrecht]

der x-Term kann nicht verschwinden , denn er entsteht aus diesen beiden Zutaten

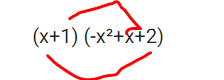
x*2 + 1*x = 3x

Answer 3

[evtldocha]

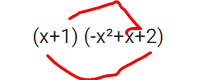
was wurde hier gemacht

... es wurde die Nullstelle x = -1 exakt geraten und anschließend eine Polynomdivision gemacht.

-x³ + 3x + 2 : (x + 1) = -x² + x + 2
-x³ - x²
------------------------------------
    + x² + 3x
    + x² + x
------------------------------------
         + 2x + 2
         + 2x + 2
------------------------------------
         0

und damit ist die Ausgangsfunktion faktorisiert in:

$f\left(x\right)=-x^3+3x+2\ =\left(x+1\right)\cdot\left(-x^2+x\ +2\right)$ und man kann den Satz vom Nullprodukt anwenden.