Integral von x^2/(wurzel(1+x^3)?
Laut einem internetrechner kommt das raus ln(x3+1)/3 das habe ich auch raus.
Mein vorgehen:
1+x^3 = y dann nach dy umgestellt und mit 3x^2 erweitert das ich es kürzen kann.
Dann steht folgendes da:
1/3x^2 integral x^2/wurzel(y) dy hier kann ich ja das x^2 raus ziehen und dann kürzen oder geht das nicht?
In meinem Buch steht aber folgendes. 2/3 Wurzel(1+x^3)
5 Antworten
Integration durch Substitution F(x)=Integral(f(z)*dz/z´
Substitution z=1+x^3 abgeleitet z´=dz/dx=3*x^2 ergibt dx=dz/(3*x^2)
F(x)=1/3Int.x^2/x^2 * z^(-0,5)*dz
F(x)=1/3*z^(-0,5+1)*1/(-0,5+1) +C
F(x)=1/(3*0,5)*Wurzel(1+x^3)+C
F(x)=1/(1,5)*Wurzel(1+x^3)+C
Hinweis: Die Integration durch die Substitution funktioniert nur,wenn z´=dz/dx=konstant ist oder sich wie hier x^2/x^2 herauskürzt
"1/3x^2 integral x^2/wurzel(y) dy hier kann ich ja das x^2 raus ziehen und dann kürzen oder geht das nicht?"
Wie kommst du darauf, 1/3 x^2 vor dem Integral hinzuschreiben?? Das musst du im Integral lassen, da es (mittels y = 1+x^3) von der Integrationsvariablen abhängig ist. Genauso kannst du x^2 nicht aus dem Integral rausziehen. Dann kannst du das aber trotzdem x^2 kürzen, da ja beides im Integral ist.
Wie du dann auf ln(x3+1)/3 gekommen bist, weiß ich nicht. Das Ergebnis im Buch stimmt.

Auch WolframAlpha liefert das als Ergebnis:
https://www.wolframalpha.com/input/?i=Integral+x%5E2%2Fsqrt(1%2Bx%5E3)+dx
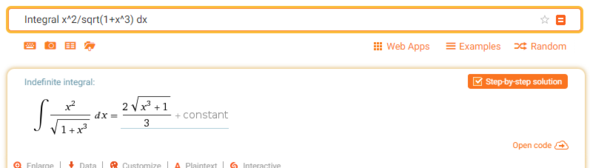

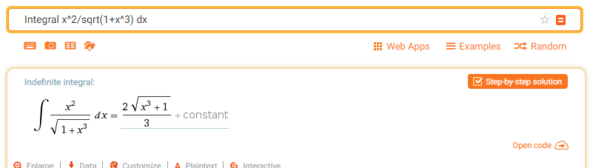
jep , ich hab mal das integral ableiten lassen. stimmt
https://www.wolframalpha.com/input/?i=f(x)+%3D+2%2F3+*+(+(x%5E3)+%2B+1)%5E0.5
Woher hast du das y?!
Stichwort Substituieren
u= 1+x^3 -> du/dx = 3x^2 -> dx=du/(3x^2)
Nun kürzt sich das x^2 weg und dein Integral lautet:
1/3 Integral (1/wurzel(u) du)
Am ende rücksubtituieren
die lösung im buch ist richtig .
dieser internetrechner sagt das
https://www.wolframalpha.com/input/?i=f(x)+%3D+(x%5E2)%2F(1%2Bx%5E3)%5E(0.5)
guck bitte , um die richtige Funktion eingegeben wurde.
Da hat das Buch eindeutig einen Fehler.
Die Lösung im Buch kann ja schon allein deshalb nicht stimmen, weil der Grad der Funktion kleiner ist als der der Ausgangsfunktion...
Grob gesagt, ist der "Grad" vom anfänglichen Integranden 2 - 3/2 = 1/2.
Nach dem Integrieren ist der "Grad" (bei der Buchlösung) 3/2. Und damit 1 größer als der vom Integranden.
[Für den "Grad": Für x gegen unendlich ist die 1 unter der Wurzel vernachlässigbar. Damit erhält man dann das gleiche Verhalten wie bei x^(1/2) bzw. x^(3/2).]
Passt doch! Ich weiß nicht, was du da erzählst, Destranix.
die lösung im buch ist richtig .
dieser internetrechner sagt das
https://www.wolframalpha.com/input/?i=f(x)+%3D+(x%5E2)%2F(1%2Bx%5E3)%5E(0.5)
guck bitte , um die richtige Funktion eingegeben wurde.
Laut diesem Link ist das Integral gleich die integrierte Funktion...
gucken, du hast nur <<result>> gesehen. Das ist noch mal die Eingabefunktion zur Kontrolle.
Gut super das dachte ich mir auch. Danke für die Hilfe :)
Wir haben es mit y gelernt anstelle von u :) das 1/3 hast du glaub vergessen aber genau auf das selbe komm ich dann ja auch :)