Gleichung dritten Grades lösen?
Folgendes bestimmtes Integral soll berechnet werden
Für k größer 0
Integral von 2 bis k (x^2+1) dx = 4/3
Folgende Gleichung dritten Grades kommt raus
0= k^3 + 3k - 18
Hat jemand eine Idee, wie man die Gleichung ohne Polynomdivision lösen kann oder die Aufgabe anders lösen kann
4 Antworten
Ich komme auch auf die Gleichung k^3 + 3 k - 18 = 0 .
Diese hat aber keine ganzzahlige Lösung.
Mit dem Plan, mittels Polynomdivision weiterzukommen, kommt man also nicht weiter. Ich würde dann zu einem Näherungsverfahren (Newton) raten, um die (einzig mögliche !) reelle Nullstelle zu lokalisieren.
(k³ / 3) + k - ((2³ / 3) + 2)) = 4 / 3
(k³ / 3) + k - (14 / 3) = 4 / 3
(k³ / 3) + k - (18 / 3) = 0
k³ + 3 * k - 18 = 0
Polynomdivision hilft nicht. Cardanische Lösungsformeln sind zu aufwendig. Ein Näherungsverfahren, z.B. das Newtonverfahren, käme infrage oder ein entsprechender Taschenrechner oder Online-Rechner.
Gut,
ist jetzt gesichert die zu lösende Gleichung, ich war derjenige der sich verrechnet hat (pardon!).
Leider haben sowohl rumar als auch gauss recht, eine Polynomdivision führt hier zu nichts da es sich bei der linken Seite um ein irreduzibles Polynom handelt.
Es wurde schon vorgeschlagen die Lösung numerisch zu bestimmen, beispielsweise mit dem Newtonverfahren. Selbst wenn Du nur mit Stift und Papier rechnest bekommst Du eine sehr ansehnliche Genauigkeit.
Wenn Du aber die exakte Lösung brauchst kannst Du die Lösungsformel für kubische Gleichungen verwenden. gauss hat zurecht darauf hingewiesen dass das etwas aufwendiger ist. Ich kann versuchen Dir dabei zu helfen, wenn es unbedingt sein muss.
Deine Umformungen sind richtig, sehr gut!
Nun hast du eine kubische Gleichung, zur Lösung von dieser hast du verschiedene Möglichkeiten.
Einsetzen und dann Polynomdivision/Horner Schema (empfehle ich!): Schau immer zuerst nach der. Tipp: Wenn es rationale Lösungen sind, dann müssen diese Lösungen auch Teiler vom Absolutglied sein (hier -18).
Newton Verfahren: Wenn es keine rationale Stellen sind, dann setzt einfach mal ein und wenn du nen guten, einfachen Wert findest, dann benutz ein Näherungsverfahren.
Lösungsformeln von Cardano: Die empfehle ich dir hier! Warum? In der Lösung kommen häufig komplexe Zahlen vor, obwohl es was reelles ist. Hier aber nicht, deswegen.
Die Formel lautet für deine Form:
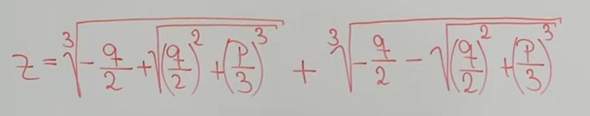
Deine Gleichung lautet: k^3+3k-18=0. Nur in dieser Form kann man diese Formel anwenden. p=3 und q=-18
Was als exakte Lösung rauskommt: https://www.wolframalpha.com/input?i=Surd%5B9%2BSqrt%5B82%5D%2C3%5D%2BCbrt%5B9-Sqrt%5B82%5D%5D&assumption=%22%5E%22+-%3E+%22Real%22
LG

Mit dem Kopfrechnen scheinen wir's heute nicht so zu haben ....