Flächenberechnung aber wieso die Formel?

Ich habe die Aufgabe soweit bearbeitet und auch verstanden aber wo ich einfach nicht drauf komme ist, wie man auf die Formel oder Gleichung der Fläche des Dreiecks in der Mitte kommt, also: „1/2k mal Wurzel k^2 - 1/4 k/2 = Wurzel 3/4 k/2“ ?

Und danach dann noch die Gleichung der blauen Fläche, wie man auf die Gleichung kommt :/

Im Grunde ab „Wichtig“ am Ende komme ich nicht mit bei der Rechnung.

Einmal die Bearbeitung: Gesucht ist der Flächeninhalt der blauen Fläche

Answer 1

[MeRoXas]

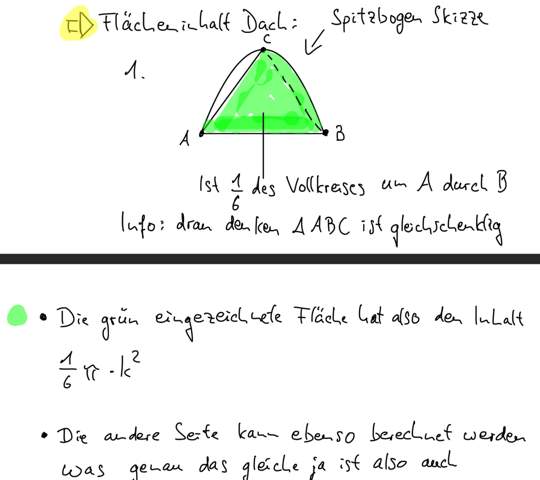
Für den Flächeninhalt des Dreiecks brauchst du ja die Formel Grundseite * Höhe / 2. Wegen der Gleichschenkligkeit des Dreiecks sollte die Grundseite bekannt sein; diese ist dann einfach k. Für die Höhe muss man etwas tricksen.

Stell dir mal vor, dass du von der Spitze bis zur Grundseite eine Linie ziehst. Diese Linie teilt das Dreieck dann in zwei rechtwinklige Dreiecke auf, die k/2 und die Höhe h als Katheten und k als Hypotenuse haben. Gemäß dem Satz von Pythagoras gilt dann k²=(k/2)²+h²

Das ganze stellt man nun nach h um:

h² = k²-(k/2)², also h² = k² - k²/4 und somit h=√( k²-(k/2)²) Wenn man jetzt den Ausdruck unter der Wurzel zusammen rechnet, steht da h=√ (k² - k²/4), bzw. h=√(3/4*k²), da k²-k²/4 eben 3/4*k² ist. Jetzt kann man aus 3/4 * k² noch die Wurzel ziehen, das kann man hier komponentenweise machen: Die Wurzel aus 3/4 ist √3 / 2, die Wurzel aus k² ist k, insgesamt also h=√3 / 2 * k.

Dadurch kommt man dann gemäß der Flächenformel auf den Flächeninhalt des Dreiecks: Dreiecksfläche = 1/2 * k * h, also 1/2 * k * √3 / 2 * k, bzw. wenn man die Reihenfolge der Faktoren ändert und die Brüche zusammenrechnet, √3 / 4 * k²

__________

Jetzt kommt meiner Meinung nach ein Fehler in der Berechnung; der Gedankengang ist hier: Spitzbogenfläche minus Kreisflächen gleich blaue Fläche. Das ist auch genau der richtige Gedanke, aber es wurden hier aber die Kreisflächen von der Dreiecksfläche abgezogen. Diese ist aber nicht die Spitzbogenfläche, da hier noch die zwei gekurvten Stückchen über dem Dreieck fehlen!

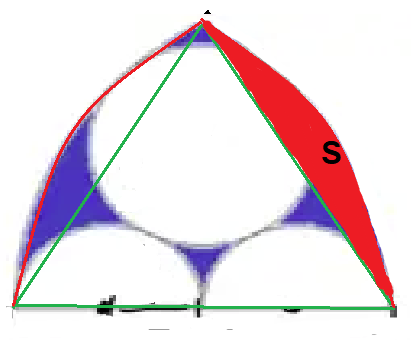
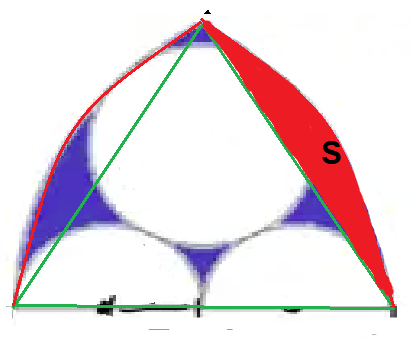
Hier nochmal ein Bild, um es etwas einfacher zu machen. Die rot ausgemalte Fläche nenne ich mal S (ich war zu faul, links jetzt auch noch auszumalen), und wenn man jetzt eben die beiden S und die Dreiecksfläche zusammenrechnet, hat man die Fläche des Spitzbogens. Wenn man aus der Spitzbogenfläche nun die ganzen Kreise rausschneidet, bekommt man genau die blaue Fläche.

_____

Hier wäre mein Vorschlag:

Für die Fläche muss nun also gelten:

$\text{Blaue Fläche}=\underbrace{\text{Dreiecksfläche + 2*S}}_{\text{Spitzbogenfläche}}-\text{ Kreisflächen}$

Dreiecksfläche? Kennen wir. Die ganzen Kreisflächen? Kennen wir. Fehlt nur noch S. das ist wieder etwas tricky.

Guck dir mal die grüne Fläche an, die in der Lösung ist. Diese ist ja mit 1/6 * k² * pi bekannt und setzt sich aus der Dreiecksfläche ( √3 / 4 * k² ) und einem Stückchen (S) zusammen, also muss doch gelten:

$\underbrace{\frac{1}{6}\cdot k^2\cdot \pi}_{\text{Grüne Fläche}} = \underbrace{\cfrac{\sqrt{3}}{4}\cdot k^2}_{\text{Dreiecksfläche}}+S$

Umstellen ergibt

$S=\cfrac{1}{6}\cdot k^2\cdot \pi-\cfrac{\sqrt{3}}{4}\cdot k^2$

Somit hat man letztendlich:

Woher ich das weiß: Studium / Ausbildung – Höheres Fachsemester

Comments

[Knoppers100092]

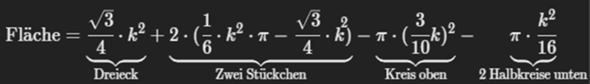
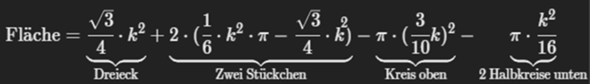
Mega Dankeschön! :) Ich werde mich später mal ansetzen und versuchen alles nachzuvollziehen und hoffentlich alles soweit dann verstehen :)