Extremstellen zusammengesetzte Funktionen?
Hallo, ich schreibe bald eine Klausur und komm bei einer Aufgabe gar nicht weiter. Undzwar soll man die erste und zweite Ableitung der Funktion f bestimmen und sie auf auf Extremstellen untersuchen. Das Problem ist ich weiß nicht wie ich weiter vorgehen soll wenn ich die 1.Ableitung gleich Null setze, wie soll ich das lösen?
a)f(x)=x*e^x
Meine Vorgehensweise:
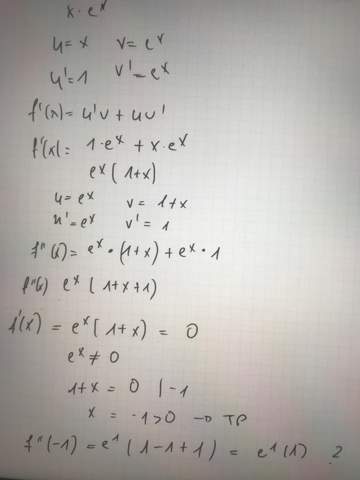
1 Antwort
wenn das die erste Abl ist
e^x*(1+x)
die kann nur Null werden , wenn x = -1 , da ein Extremum
denn e^x kann nicht Null werden.
Lösung durch Argumentieren, kein klassisches Rechnen wie bei pq
.
.
hast du ja auch korrekt
.
f''(x) = e ^x ( 2+x)
mit x = -1
e^-1 * (1) = e^-1 = 1/e = positive Zahl , TP.
.
Und WendePunkt bei x = -2
.
gucken
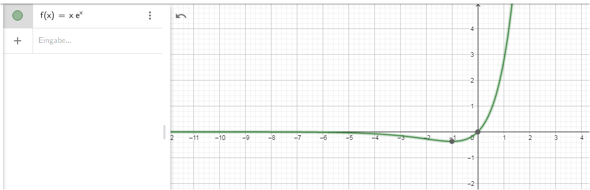
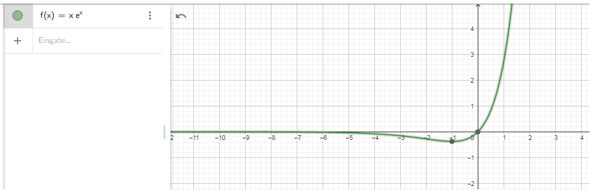
passt
Ich hab da als 1.Ableitung -1*e^x+(-x+2)*e^x raus also zusammengefasst e^x(-1x-2) und davon die 2.Ableiting wäre -1x-2 aber wie gehe ich dann voran wenn ich die 2.Ableitung gleich null setzte?
mit x = + 2 wird das null
Deine Ableitungen sind doch korrekt : f'(x) = e^x * (x+1) und f''(x) = e^x * (x+2) !
diese Ableitungen sind nicht die von x*e^x !!! ............und wenn die erste schon (-1x-2) ist kann es nicht auch die zweite sein !
Wie wäre das bei der Funktipn f(x)=(-x+2)*e^x ?