Stimmt es, dass man sagen kann, dass die Nullstellen der Ableitung auch die Extremstellen der Funktion sind?
Hallo,
ich lerne gerade das Thema Ableitungen, Funktionen etc. Stimmt es, dass man sagen kann, dass die Nullstellen der Ableitung auch die Extremstellen der Funktion sind? Wenn also nach den Extremstellen der Funktion gefragt ist, kann man die Funktion dann ableiten und die Nullstellen bestimmen und das dann als Ergebnis aufschreiben? Unten eine Beispiel Aufgabe wie ich es gerechnet habe.
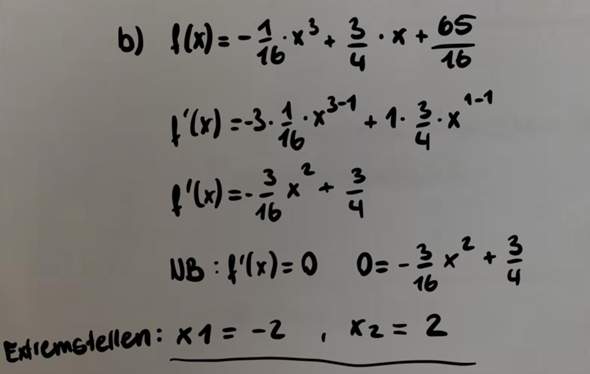
6 Antworten
Ja, um die Extremstellen zu finden, bestimmt Du die Nullstellen der ersten Ableitung:
Extremstellen berechnen - Hochpunkte Tiefpunkte bestimmen - Teil der Kurvendiskussion - YouTube
Ein inneres Extremum hat die Steigung 0, die Aussage ist aber nicht umkehrbar.
Tipp: Ableitung an der Stelle auf Vorzeichenwechsel untersuchen.
Für die Extremstellen, ist es notwendig, dass die Ableitung = 0 ist.
Hinreichend ist das aber nicht, auch bei einem Sattelpunkt ist die Ableitung = 0
Ja im Prinzip schon. Durch die erste Ableitung kannst du dir durch die NEW-Regel merken was zu was wird:
Man schreibt NEW drei mal versetzt untereinander und kann sehen was zu was wird
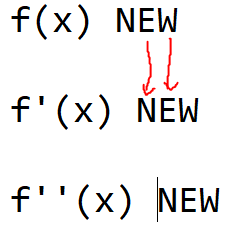
Wie du siehst wird eine Extremstelle zu einer Nullstelle und ein Wendepunkt zu einer Extremstelle. Um die Extremstelle zu finden setzt du f'(x)=0 und rechnest aus.
Hier ein tolles Video dass das umfassend erklärt
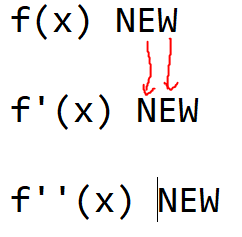
Nein.
Nullstellen der 1. Ableitung sind NICHT zwangsläufig immer auch Extremstellen der Funktion.
Bsp.: f(x)=x³
f'(x)=3x² Nullstelle der Ableitung: x=0
Aber: x=0 ist KEINE Extremstelle von f(x)=x³