Kreis – die neusten Beiträge

Hi, ich bin letztes von Amsterdam über Afrika nach Kapstadt geflogen und auf dem Weg dahin habe ich abundzu mal aus dem Fenster geguckt. Irgendwo in Zentralafrika sind mir dann komisch Kreise auf dem Boden aufgefallen. Ich weiß leider nicht mehr genau wo es war, aber sollte irgendwo zwischen Tschad und Libyen oder so. irgendwo dort gewesen sein. Was sind das für Teile?

So nen komischer Typ behauptet ein kreis hätte unendlich Ecken. Stimmt das? Hat ein Kreis wirklich ecken???

Wenn man einen Kreis zeichnet gibt es einen Anfang und ein Ende, auch wenn man es noch so genau zeichnet hat man irgendwo angefangen und hört auch irgendwo wieder auf. Sollte ein Kreis nicht aber genau das nicht haben?

Ich soll in einen Kreis, wo nur der Mittelpunkt gegeben ist, ein rechtwinkliges Dreieck einzeichen. Dieses soll ich so einzeichnen, dass alle Drei Ecken auf der Kreislinie liegen. Wie funktioniert das?

Hallo :-) ich bin in der 8. Klasse und schreibe Morgen eine Mathearbeit, und habe heute einen Pädagogischen Tag, heißt, ich habe Schulfrei, was sich natürlich gut zum Mathe lernen anbietet (auch wenn draußen wunderschönes Wetter ist ;O). Jedenfalls, habe ich hier eine Aufgabe (es geht darum, den Oberflächeninhalt eines Stabs auszurechen). Guckt euch vitte mal die Aufgabe an, bzw. Die formel : O= 2G + M = 2•1^2•pi+ 30÷pi • 2pi. Ich weiß, dass G in dem Fall 1^2•pi ist, und M 30÷pi•2pi, denn M= U•h. H ist in em fall 30÷pi, und U = 2pi•r. Lange rede kurzer Sinn: warum schreiben wir nur 2pi, anstatt 2pi•r ? Danke im vorraus :-)

hallo zusammen ich habe ein paar fragen bzw. vermutungen und ich weiß auch die antworten ob sie richtig sind oder falsch. 1. wenn man den mittelpunktswinkel verdoppelt ,verdoppelt sich auch die dazugehörige Kreisbogenlänge -> das stimmt ja, aber wieso ? 2. ein viertel des mittelpunktswinkels ist ein viertel der fläche des kreisausschnitts -> das stimmt auch aber hängt es damit zusammen das wenn man den mittelpunktswinkel verkleinert der kreisausschnitt auch kleiner wird bzw. die fläche des kreises ? 3. vervierfacht man bei gleichbleibendem mittelpunktswinkel des radius, so vervierfacht dich die länge des kreisbogens. -> dies stimmt auch da bin ich mir sehr sicher. also das heißt ja dann das sich der kreisbogen sich immer mit der größe des mittelpunktswinkels ändern würde aber wenn dann ändert er sich dann auch nicht immer gleich viel oder?

Danke im voraus

Ich habe versucht i-wie herauszubekommen was das ist dabei bin ich auf die Blaufeld Entoptik gestoßen, die aber besagt dass es gelbe schnelle "Würmchen" sind. Allerdings sehe ich nicht nur die sondern auch durchsichtige langsame Kreise mit weißem Rand die (>bin mir nicht so sicher<) glaub ich auch außerhalb eines blauen Hintergrundes auftauchen. Vieleicht ist es ja doch das selbe was ich aber nicht glaube und ich habe auch keine Probleme mit meinen Augen oder so, ich denke es lässt sich genauso erklären wie das andere Phänomen. Also was denkt ihr was das ist? Danke im voraus

meine freundin hat gerade eine klassenarbeit über das thema geschrieben und war sich wegen einer aufgabe nicht sicher und wüsste gerne wie der richtige rechenweg lautet. ich konnte ihr auch nicht weiterhelfen also frage ich euch: du hast eine quadratische pralinenschachtel (fläche angegeben). wieviele pralinen (ENTWEDER radius,durchmesser oder umfang ist angegeben) passen in die schachtel ??? wie lautet der RECHENWEG ? danke schonmal

Ich weiß das gF keine Hausaufgabenhilfe ist aber ich komme hier wirklich nicht weiter! Hier ist ein Quadrat und innen drinne ein genau passender Kreis. Die Aufgabenstellung: "Berechne den Verschnitt, der beim Ausstanzen der Kreise aus einem Quadrat mit a=80cm jeweils übrig bleibt". Meine Frage zu all dem ist: Beträgt der Umfang des Kreises auch 80 cm?

Moin

was bedeutet bei Android der Kreis mitm Strich in der Mitte oben links?

Netz ist jedenfalls vorhanden!

Hey, Ich krieg es einfach nicht hin die Formel so umzustellen, dass ich alpha raus bekomme. Gegeben sind A und b (Flächeninhalt des Bogens, Bogenlänge)

Steht oben danke

Ich möchte einen Kreis in drei gleich große Teile in Gimp teilen. Wie kann ich das bewerkstelligen? Eine Suche im Netz hat keine brauchbare Lösung geliefert.

1. Kreisbogen: b= 2• π• r• α/360° bzw. ...= π• r• α/180°
2. A des Kreisausschnittes: A= π• r²• α/360°

Die ersten beiden Formeln verstehe ich gut und kenne deren Herleitung sowohl rechnerisch als auch zeichnerisch, jedoch weiß ich nicht weiter, wie ich diese beiden Formeln irgendwie gleichstellen soll, damit 1/2• b•r herauskommt. Kann mir da jemand helfen? Am besten wäre ein schrittweiser Rechenweg.

Danke im Voraus für Eure Mühe!

Hallo,

warum ist Pi gerade 180°, also der halbe Umfang vom Einheitskreis und nicht 360° und damit der volle Umfang?

Wo kommt es her, dass es eben nur die Hälfte ist?

Vielen Dank!

Alsoo meine Frage: Was bedeutet dieses Symbol ? Hat es überhaupt eine Bedeutung ?

Es gibt anscheinden einen klaren Beweis dass Pi = 4 ist... Fail?

Naja, theoretisch:

Man nehme einen Kreis (Durchmesser = 1, Nach Archimedes sollte der Umfang Pi sein, das wird aber widerlegt). Um den Kreis macht man ein Quadrat mit dem Umfang 4 (Jede Kante genau 1 = Durchmesser, Kreis). Dann nimmt man die Ecken aus dem Quadrat raus sodass des Umfang 4 bleibt. Dies wiederholt man nun in die Unendlichkeit, Unendlich = Perfekter Kreis. Aber der Umfang bleibt 4.

Ergebnis: Pi = 4. Nun die Frage: Warum ist Pi immer noch diese bescheuerte 3.14 Dings wenn es einen Beweis für die Theorie Pi = 4 gibt? Sogar ein sehr klarer Beweis!

Ziemlich viele kennen die Zahl Pi (3,14.....) Doch welche Ziffer oder Zahlenfolge kommt am häufigsten in Pi vor, klar is Pi eine reine Zufallszahl, doch es kann ja nicht in der unendlichen Zahl jede Ziffer gleich oft vorkommen.

Hier mal Pi mit 10 Mio Nachkommastellen (auf STRG+F ist die Suche)

http://www.aip.de/~wasi/PI/Pibel/pibel_10mio.pdf

Ich versuche eine Powerpoint Presentation zu erstellen für meinen Vortrag über Atommodelle. Ich bin leider nicht sehr versiert im Umgang mit Powerpoint und nun habe ich das Problem das ich den Atomaufbau mit Kreisen darstellen will und diese sollen sich berühren aber nicht überlappen. Ich krieg es einfach nicht hin das das gut aussieht, auch nicht mit dem Hilfslineal. Entweder überlappen sich die Kreise oder berühren sich nicht. Kann mir bitte jemand sagen wie ich das hinbekomme, dass es keine Lücke hat aber sie sich auch nicht überlappen.

Danke im Voraus MfG gnamf123

Ich hab ein richtig grosses Problem :( ich Brauche einen Zirkel um die Hausaufgaben zu lösen (Geometrie) ich habe aber keinen !!! Die Läden sind schon zu . Ich muss es erledigt haben bis morgen . Sonst muss ich nachsitzen :/ Hilfe ??? Wie, was ???? Kann man einen Zirkel basteln ??? Oder kann man Perfekte Kreise ohne Zirkel machen ??? (Ohne runde Gegenstände ?? Weil es eine bestimmte Grösse haben muss??) DANKE :)

Ich glaube, die Aufgaben sind sehr einfach, aber ich komme leider nicht drauf. Wir haben das Thema erst angefangen. Jedenfalls ist d immer 8 cm lang. Bei a) ist ja der Radius von dem großen Halbkreis 4 cm und von den zwei kleinen 2 cm, oder? Aber wie rechne ich dann den Umfang und Flächeninhalt aus? Wäre sehr nett, wenn mir jemand das genau erklären könnte.

hallo! heute auf der strasse habe ich ein auto gesehen das mir keinesfalls bekannt vor kam hinten an diesem wagen war ein schwarzer stier in einem kreis zu sehen wisst ihr welche automarke das war?

danke im voraus - LinkinParkBiD -

Hallo, wie erstelle ich in Photoshop CS3 einen Kreis mit Durchmesser aber in mm (Millimeter) ich kann zwar feste Größe einstellen aber dann kann ich nur Pixel x Pixel angeben :/

Danke schonmal

Liebe Community,

Ich habe ein Problem bei der Physik Hausaufgabe, da ich glaube, dass hier zu wenig gegeben ist.

Die Frage lautet: Wie groß ist die Geschwindigkeit eines Körpers am Äquator bei der Kreisbewegung, die durch die Erdrotation hervorgerufen wird? (Erdradius: 6 370 km)

Vielen Danke, für eure Hilfe :)

Mfg. Vulc.

was bedeutet ein kreis mit strich durch die mitte symbolisch? danke.

Man kann ja z.B. herausfinden in welchem Bereich die Postleitzahlen eines Landes liegen, wie z.B. das Saarland. Man kann auch z.B. herausfinden, in welchem Bereich die Postleitzahlen einer kreisfreien Stadt liegen, wie z.B. Saarlouis von 66711 bis 66740. Wie findet man heraus in welchem Bereich die Postleitzahlen eines Regierungsbezirks oder eines Kreises liegen, oder überschneiden die sich?

Aus einer quadratischen Stofffläche wird ein größtmöglicher Kreis ausgeschnitten. Wieviel Rest bleibt in Prozent übrig.

Bitte um Hilfe komme einfach nicht weiter.

???????????????????

Ich male gerade ein geometrisches Gebilde und habe folgendes Problem: Auf einem Kreis möchte ich 5 Punkte machen, die den gleichen Abstand von einander haben. Wie mache ich das? Der Radius ist 4,8 cm und der Umfang 30,16 cm. Danke schon mal im Vorraus!

Weiß jemand wie ich einen exakt runden Kreis mit Paint.NET malen kann?

Ich sehe hier nur das Ellipsen-Werkzeug, welches frei bewegliche Kreise erstellt, ich brauche aber einen absolut runden.

Ich brauche ganz schnell Hilfe ,weil ich meine Hausaufgaben noch machen muss also bitte schreibt schnell die aufgabe lautet: M (2/2) r 2,7 cm. Gib jewals an ob, die Geraden durch die Punkte einer Passante Tangete oder sekante an den Kreis ist und bestimme die abstände der geraden von M. a) P(5,5/0) ; Q ( 7/3,5) b) C ( -1,5/0,5) ; U (4,5/-0,5) c) V ( 4,5/6) T (-1/ 3,7) d) Gib die Koordinaten zweier Punkte L und K an, sodass die Strecke KL Durchmesser des Kreises ist. Bitte schnell antworten und möglichst genau danke :) LG Und muss ich mehrere koordinatensysteme zeichnen oder nur eins? :-(

hallo,

wenn man einen Bewerbungsbogen ausfüllen soll, steht immer Geburtsort/Kreis/Bundesland.

Meine Frage wäre, was Kreis heißen soll?

Danke im voraus.

Ich schreibe Morgen eine Mathearbeit und komm mit einer Aufgabe gar nicht klar und zwar " "Der große Zeiger einer Uhr ist 12 cm , der kleine Zeiger 7 cm lang. a) Berechne die Strecke ,die die Spitze des großen Zeigers in einer Stunde zurücklegt . b)Welchen Weg legt die Spitze des kleinen Zeigers an einem Tag (einer Woche) zurück ? (auf der Abbildung ist eine Uhr zu sehen der große Zeiger ist auf 51 min. der kleine Zeiger steht auf 14:00 Uhr ) das ist auf der Abbildung zu sehen , es wäre toll wenn mir jemand weiterhelfen würde sehr wichtig bittteee, danke :)

Hi! Ich grübel grade über eine Matheaufgabe nach ( schreibe morgen eine wichtige Klausur) also: Habe einen Radius von einem Kreis. Dieser beträgt 1,43cm Der Umfang ist ebenfalls angegeben: 9cm Den Flächeninhalt habe ich anhand von r² x pi errechnet. Das ergibt bei mir 6,42cm. Mir stellt sich nun die Frage, kann es sein, dass der Umfang einen größeren Wert als der Flächeninhalt hat? Bitte schnell um eine Antwort! Grüße Loo

erstemal Hallo an die Leute hier :)

ich muss jetzt wirklich mal eine Frage zu einer Hausaufgabe stellen,, weil ich zerbrech mir heut schon den Kopf und weiß trotzdem nicht weiter ._.

Wir haben gerade Kreis- und Kreisringe dran, weiß aber nicht wie ich das rauskriege oder wie der Rechenweg ist:

"Von einem Stoffrest der Breite 1,40m und der Länge 1,60m soll eine möglichst große kreisrunde Tischdecke hergestellt werden. Wie viel Prozent Verschnitt entstehen?"

Kann mir jemand helfen?

Bitte nicht antworten "Das ist kein Hausaufgaben Forum" oder sowas, ich hab echt lange probiert aber ich begreifs einfach nicht ._.

Bitte auch die Frage nicht löschen ._.

LG

Meine Mathelerhrerin heute so : Malt einen ovalen Kreis. Aber wenn er oval sein soll, dann ist es doch kein Kreis? Kreise sind doch immer rund? Sonst könnte man ja sagen ; Malt ein Viereckigen Kreis ?! hä?

Ich soll eine Gruppenstunde für Grundschüler von 6-9 Jahren halten. Es sollen Kreisspiele sein. Kennt ihr eher unbekannten Spiele? Denn Kreisspiele werden dort häufiger gespielt und es sollen nicht immer dieselben drankommen.

Der Flächeninhalt eines Kreises beträgt ja A = pi * r².

Könnte man diesen auch durch Integral bestimmen, indem man die Kreisgleichung r² = x² + y² z.B. beim Einheitskreis für r=1, also 1 = x² + y² nach y umformt und dann nach x integriert, also y= Wurzel(1-x²) und dann Integral von -1 nach +1. Damit könnte man dann auch noch pi bestimmen. Geht das?

was bedeutet das plus in dem kreis ?? danke ! ;D

(leider etwas schlecht geworden ;D)

Hallo, wir schreiben am Mittwoch eine Mathearbeit und da wir vorher nur noch 1 Stunde Unterricht haben, wollte ich fragen, ob mir jemand erklären kann, wie man, wenn man einen Kreis gegeben hat, dass innere Quadrat ausrechnet. Ich glaube man braucht den Pythagoras, Euklid dazu, aber ich weiß nicht wie :(

Ein Lehrer vom Gymnasium meinte ein Kreis hat unendlich viele Ecken stimmt das?

Ich benötige eure Einschätzung für eine Ausarbeitung.

Deshalb bitte eure Antworten in Umfrageform geben:

"Ein Greis ist für mich eine Person ab ... Jahren."

hallo zusammen ich habe bald ein vorstellungsgespräch zur verwaltungsfachangestellten beim Kreis. was kann ich denn von mir preisgeben ohne das es schlecht rüber kommt? was sind gute schwächen und stärken? es soll ja nicht so eingenommen wirken. wer hat selbst schon ein vorstellungsgespräch zur verwaltungsfachangestellten gehabt und kann mir sagen was die alles gefragt haben?

freue mich über jede antwort.

danke

weiss das jemand : in welchemverhältnis stehen flächeninhalt eines quadrates zu dem eines kreises wenn ihre umfänge übereinstimmen?

Ich suche eine automarke dessen symbol ein kreis mit einem senkrechten Strich dafurch ist

Wenn man ´mit jemanden chattet und jemand online ist, ist ein grüner Kreis zu sehen. Und manchmal ist da ein grauer halbrunder Kreis. Was bedeutet ist?

Sehe ich in letzter Zeit Häufiger, ähnlich wie das "A"narchie Symbol. Aber wofür steht (V) ?

-> ()=Kreis :D

Wie teile ich einen Kreis mit Zirkel und Lineal in fünf gleiche Segmente?

Also, ich wüsste gerne, wie man kleine Kreise (mit 1-2 cm Durchmesser) sauber zeichnen kann!

Mit einem Zirkel geht das nicht gerade gut, die sind einfach zu klein!!!

Geht das denn mit einer Schablone oder wird das bei dieser Größe schwierig?!

Danke schonmal!!!:)))

Hallo,

ich habe mir für Morgen mit einem PC-Kühler (Im Bild MOTOR) und 2x 9V batterien einen kleinen Ventilator gebaut. Das eine + der einten Batterie habe ich mit dem Motor, und von der anderen Batterie das - habe ich mit dem anderen Draht des Motors verbunden. Die Roten Kabel wären von den anderen 2, noch nicht gebrauchten Polen der Batterie.. Wenn ich die 2 verbinde, läuft der Strom und der Motor dreht genügend schnell.

Wenn ich aber das rote Kabel getrennt habe, läuft natürlich der Motor nicht.. Wird aber trotzdem Strom von der Batterie irgendwie verbraucht (Habe die Kabel angelötet)?

Herzlichen Dank

hoffe ich habs verständlich Erklärt + Skizze

Ist das möglich?

Frage: siehe oben! :)

Hoffe ihr könnt mir helfen :)

Heey , bei dieser Aufgabe habe ich noch nicht einmal ein Ansatz gefunden -.-
Tut mir leid, dass ich soviel frage. Aber ich komm einfach nicht klar..

Berechne den Flächeninhalt und den Umfang der gefärbten Fläche.

Danke..

Hallo!

Weiß jemand wie man ein Kreiß in 16 bzw. 8 gleiche Teile teilt? Wenn ja wie macht man es?

(Nicht in irgendein Programm sondern auf Papier) Danke schon Vorraus!

Hey Leute. Ich verzweifle gerade an einigen Matheaufgaben.

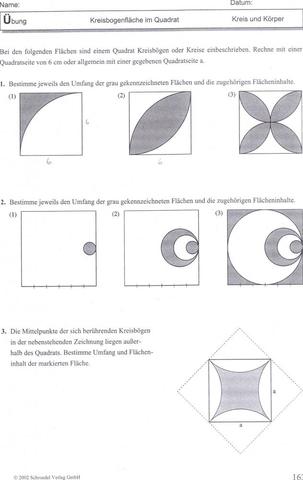
Aufgabe 1 Nummer (1) (siehe Datei) haben wir zwar schon in der Schule gelöst, aber ich komme einfach nicht selbst auf das Ergebnis.

Also, Aufgabe ist es, Umfang und Flächeninhalt der grauen Fläche zu berechnen. Flächeninhalt hab ich, aber ich komme nicht auf den Umfang.

ich bin so vorgegangen:

1. Umfang Quadrat = 4*a bzw. 4*6 (a = 6)

2. Umfang Viertelkreis =( 2*pi*a) : 4 bzw. (2*pi*6) : 4 (a = 6)

3. Umfang graue Fläche = Umfang Quadrat - Umfang Viertelkreis = 4*6 - 9.42 = 14.58

Dieses Ergebnis ist aber falsch. Da müsste etwas mit 21 rauskommen. Was habe ich falsch gemacht? Und hat jemand einen Ansatz für Aufgabe 1 Nummer (2)? Oder für Aufgabe 2?

Aufgabe:

In einem Park ist ein kreisrunder Teich. Im Abstand von 50 cm vom Rand des Teiches ist ringsum ein Schutzgeländer. Es ist 22 cm lang.

Unmittelbar vor dem Geländer ist ringsum ein 2 cm breiter Asphaltweg angelegt.

a). Wie viel Quadratmeter ist die Wasserfläche groß ?

b). Wie viel Quadratmeter ist die asphaltierte Fläche groß ?

Kann mir jemand helfen?

Joa, eigentlich steht alles schon daoben. Also, wo liegt der genaue Unterschied? Irgendwie sind alle anderer Meinung und Google hilft auch nicht =(

was ist denn jetzt größer, kreis oder bezirk? habs auch schon gegoogelt... aber niix gefunden..

Wäre 100 Grad nicht sinnvoller gewesen, da es in diesem Fall mit Prozent übereinstimmen würde?

Wie & mit welchem Programm bekommt man solche "Lichtpunkte" wie auf dem folgendem Bild hin?

Liebe Grüße, AliceMary ^^

Worin besteht der Unterschied zwischen einem Kreis und einem Landkreis, oder ist das erste nur eine Abkürzung?

Hallo ! ich habe ein Problem, ich weiß nicht wie man den Umfang und den Flächeninhalt berechnet. Könnte mir einer sagen wie ich das machen kann ? Größe siehe Bild (korrektur, keine 37 cm sondern m ! )

ich wollte nämlich was auf schwedisch schreiben.. da ist so ein a mitn ° drüber.. was muss ich für tasten drücken, um den kreis ÜBER den buchstaben zu bekommen? Bitte helft mir...

ist der radius bei einem kreis, immer die hälfte vom durchmesser???