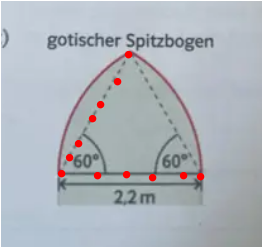
Wie rechne ich die Bogenlänge eines gotischen Spitzbogens aus?

Kann mir das vielleicht einer erklären?
4 Antworten
Ein Kreis hat den Umfang U = 2*pi*r - ein Kreisbogen mit Mittelpunktswinkel alpha entsprechend U_b = 2*pi*r*alpha/360. Der gotische Spitzbogen hier besteht aus 2 Kreisbögen mit Mittelpunktswinkeln alpha = 60 Grad und Radien r = 2,2m. Wenn man pi näherungsweise gleich 3 setzt, ergibt sich für die Bogenlänge des Spitzbogens näherungsweise:
L = 2*U_b = 2*2*pi*2,2*60/360 = 4*pi*2,2*1/6 = 4*3*2,2/6 = 4,4
Voraussetzung: Es handelt sich um einen normalen Spitzbogen, bei dem der jeweilige Kreismittelpunkt der jeweils gegenüberliegenden Dreiecksecke entspricht. Dann gilt:
b / (2 * 2,2 * π) = 60° / 360° = 1 / 6
Das Dreieck ist gleichseitig. Es gibt aber Bögen, bei denen der Kreismittelpunkt nicht in einer Dreiecksecke liegt und damit der Radius größer oder kleiner ist, als eine Dreiecksseite.
ein Kreis hat ja 360Grad, diese 360Grad kannst du auch als 2 pi ausdrücken. Grund hierfür ist der Einheitskreis, dessen Umfang even genau 2pi ist.
360 Grad ist also 2pi.
-> 180 grad ist Pi (Dreisatz)
Ein Kreisausschnitt von 60 grad ist also pi/3.
du hast zwei Kreisausschnitte mit je 60 Grad, also hast du zwei mal die Länge pi/3.
und, da dein Radius die Zahl 2,2 ist musst du das Ergebnis noch mit 2,2 multiplizieren.
also in deinem dann 2*3/3 *2,2= 2*2,2=4,4.
weil die Winkel alle 60° sind , ist es ein gleichseitiges Dreieck

anhand dieser Information erkennt man , dass AC und AB beide Radien eines Kreises um A sein müssen, weil die Strecken gleichlang sind .
.
Damit ist der Bogen 1/6 des Kreisumfangs , weil 60 1/6 von 360 ist
.
1/6 * 2*pi*2.2
weil 60 müssen doch AB und AC gleichlang sein