Wie kann ich die Schnittpunkte von Parabel p und Gerade g berechnen?

Wenn jemand das berechnen kann, dann wäre ich Ihnen sehr dankbar!

Edit: Schnittpunkt... nicht Scheitelpunkt

Comments

[Kalkablagerung]

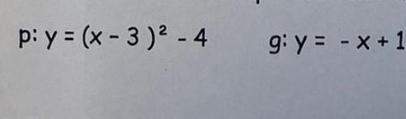
Den Scheitelpunkt oder die Schnittpunkte? Weil eine Gerade hat keinen Scheitelpunkt

[William338]

Du hast recht! Ich habe es gearbeitet

Answer 1

[Kalkablagerung]

Einen Schnittpunkt berechnet man, indem man die beiden Funktionsgleichungen gleichsetzt. Man kann sich das so vorstellen, dass man ja den oder die Punkt(e) sucht, bei dem beide Funktionen gleich sind: $\left(x-3\right)^2\ -\ 4\ =\ -x\ +\ 1$ Jetzt ist es nur noch umstellen; als erstes müssen die Klammern weg: $x^2\ -\ 6x\ +\ 9\ -\ 4\ =\ -x\ +\ 1$ Zusammenfassen: $x^2\ -\ 6x\ +\ 5\ =\ -x\ +\ 1$ Sodass, eine Seite 0 wird, damit man PQ-Formel anwenden kann (oder Mitternachtsformel, wie du willst): $x^2\ -\ 5x\ +\ 4\ =\ 0$ $x1,2\ =\ -\frac{\left(-5\right)}{2}\pm\sqrt{\left(\frac{\left(-5\right)}{2}\right)^2\ -\ 4}$ $x1\ =\ 4$ $x2\ =\ 1$ Beide x-Werte setzt du nun in die ursprüngliche Funktion ein (egal welche, da sie ja an der Stelle gleich sind): $g:\ y\ =\ -4\ +\ 1\ \ =\ -3$ Der erste Schnittpunkt lautet also S1(4|-3) $g:\ y\ =\ -1\ +\ 1\ =\ 0$ Der zweite lautet S2(1|0)

Ich hoffe, ich konnte helfen! Bei Fragen gerne fragen!

Woher ich das weiß: Hobby

Comments

[William338]

Danke! Das was sehr hilfreich!!!

Answer 2

[Sophonisbe]

Wie kann ich die Scheitelpunkte von Parabel p und Gerade g berechnen?

Bei p brauchst Du nichts berechnen. Bei der gegebenen Scheitelpunktform kannst Du den Scheitelpunkt einfach ablesen.

Bei g solltest Du kurz über die Begriffe "Gerade" und "Scheitelpunkt" nachdenken. Dann entfällt auch hier das Rechnen. :)

Woher ich das weiß: eigene Erfahrung

Answer 3

[DerRoll]

Bitte stelle die komplette Aufgabe ein, ohne Interpretationen deinerseits. Wie @Sophonisbe bereits festgestellt hat hat eine Gerade keinen Scheitelpunkt.

Woher ich das weiß: Studium / Ausbildung – Dipl.Math.

Comments

[William338]

Ja... Ich habe es korrigiert

[DerRoll]

@William338

Ah ha. Dann setze doch p(x) = g(x), stelle zu einer quadratischen Gleichung um und verwende die bekannten Lösungsformeln.

[William338]

@DerRoll

Dankeschön:)!

Answer 4

[fires609ae]

Bei p ist der Scheitelpunkt S(3|-4). Das kannst du einfach ablesen. Das was in der Klammer steht da kehrst du immer das Vorzeichen um