Wie kann ich die Eigenwerte effizienter berechnen?
Ich habe das Gefühl, dass ich die Eigenwerte viel zu umständlich berechne.
Habt ihr evtl. Tipps/Tricks?
Mein Vorgehen:
Nach der zweiten Zeile entwickeln (siehe Foto).
Daraus bekomme ich schon mal λ1=1.
Dann Nullstelle erraten für Polynomdivision. Gibt mir λ2=1.
Dann Polynomdivision.
Dann Mitternachtsformel. Gibt mir λ3=1, λ4=13
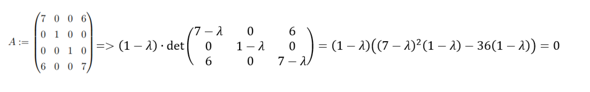
Glaube der Trick liegt darin, nochmal nach der zweiten Zeile zu entwickeln in der Determinante statt mit Sarrus auszurechnen.
3 Antworten
Das mit dem Nullstellenraten und der Polynomdivision kannst du dir ersparen, indem du einfach erkennst, dass du noch (1- λ) ausklammern kannst. Des Weiteren hilft die dritte binomische Formel dabei, nicht ausmultiplizieren und Mitternachtsformel anwenden zu müssen.
[(1 - λ) ausklammern und mit dem vorderen (1 - λ) zu (1 - λ)² zusammenfassen]
[Erkenne, dass 36 = 6² ist, um dann die dritte binomische Formel a² - b² = (a - b) ⋅ (a + b) mit a = 7 - λ und b = 6 verwenden zu können.]
Daran kann man nun relativ angenehm ablesen, dass 1 ein Eigenwert (mit algebraischer Vielfachheit 3) ist und 13 ein Eigenwert (mit algebraischer Vielfachheit 1) ist.
Statt Polynomdivision kannst Du natürlich auch die kubische Gleichung direkt schlachten. Oder einfach weiterraten — wenn die Nullstellen ganzzahlig sind, dann müssen sie ja ein Teiler des konstanten Gliedes sein, weil das das Produkt aller Nullstellen ist.
Diese Methode zum Lösen von Eigenwerten ist nicht besonders effizient. Wenn man es mit dem Computer macht, verwendet man ganz andere Verfahren (z.B. Jacobi, obwohl es noch Besseres gibt). Allerdings spielen die ihre Vorteile erst bei größeren Matrizen aus und sind fürs händische Rechnen auch ziemlich beschwerlich.
Glaube der Trick liegt darin, nochmal nach der zweiten Zeile zu entwickeln in der Determinante statt mit Sarrus auszurechnen.
Ja, man kann den gleichen Trick auch zweimal anwenden :-)