Funktionsgleichung quadratische Funktion?
Hey Leute,
brauche Hilfe.
Schreibe morgen Mathe und muss wissen wie man folgende Aufgabe berechnet:
,,Bestimmen Sie die Gleichung der quadratischen Funktion, von der bekannt ist: Nullstellen 6 und 0; y - Wert des Scheitelpunktes: 10
Hoffe ihr könnt das gut erklären.
LG
4 Antworten
zeichne es dir doch auf mal.
Sie geht durch 0 und 6 an der X-Achse.
Der Scheitelpunkt ist bei 10.
Das heißt bei der Mitte von 0 und 6 nämlich 3 ist der Scheitelpunkt.
S(3/10)
Sie ist außerdem negativ, bzw geht nach unten.
f(x) = -1.11111111 (x-3)^2 + 10
Wenn die beiden Nullstellen schon gegeben sind, kannst Du sofort mit einem faktorisierten Ansatz beginnen:
Bleibt noch "a" zu bestimmen. Da sich der Scheitelpunkt stets genau in der Mitte der beiden Nullstellen befindet, sind die Koordinaten des Scheitelpunkts x=3 und y=10, also S(3|10). Damit bestimmt man "a"
Also:
(Ausmultiplizieren darfst Du das selbst, falls das gefordert sein sollte)
Skizze:
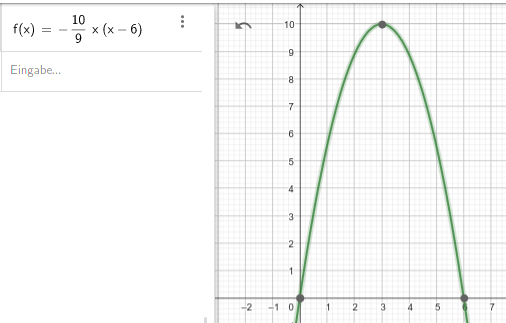
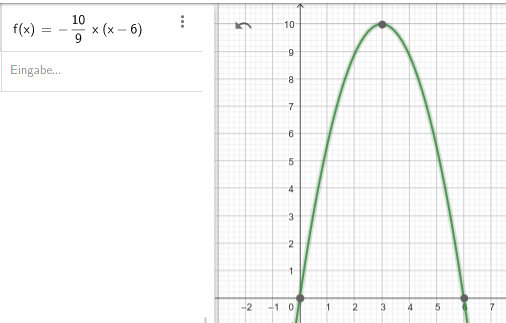
f(x) = a*(x-0)(x-6) ist der Ansatz mit den Nullstellen
.
Weil der SP genau zwischen den Nullstellen liegt , sind sein Koordinaten (3/10)
Einsetzen für a
10 = a*(3-0)(3-6)
10 = -9a
hi,
die allgemeine Form einer quadratischen Gleichung ist:
f(x)=a(x−x1)(x−x2)
x1 und x2 sind hierbei die Nullstellen. Setzt man diese aus der Aufgabe ein erhält man:
f(x)=a(x−0)(x−6)
Nun kannst du den y und x Wert des Scheitelpunkt (3|10) einsetzen um a auszurechnen:
10=a(3−0)(3−6)
10=a(3)(−3)
10=−9a
a=−9/10
für die quadratische Funktion erhältst du damit:
f(x)=−9/10(x)(x−6)
oder wenn du es aus multiplizierst und kürzt:
f(x)=−9/10 x²+3/20x