Fourierreihe integral auflösen?
Hi wie komme ich vom blau markierten auf die untere Zeile, also wie löst man das integral auf, kann mir das jemand vorrechnen
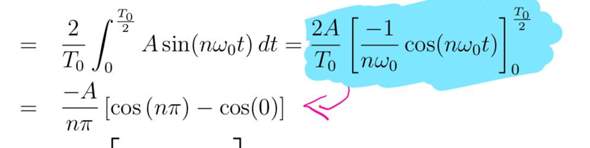
2 Antworten
Es gilt (per Definition):
Wenn wir das nun einsetzen, erhalten wir:
Nicht von t abhänigige Faktoren dürfen vor die Klammer gezogen werden.
Nun wird eine Beziehung zwischen der Periode T_0 und der Kreisfrequenz omega_0 ausgenutzt.
Damit wird ein Ausdruck generiert, der nur noch Perioden und keine Frequenzen mehr enthält.
Bei der oberen Umformung wurde im Vorfaktor die "2" und das T_0 gekürzt. Die Cosinusargumente wurden bereits mit den Grenzen besetzt. Im nächsten Schritt kann das Cosinusargument auch zusammengekürzt werden. Wieder wird die 2 und das T_0 angegriffen. Es verbleibt.
Damit wäre Deine Frage erschöpfende beantwortet. Doch es geht noch weiter.
Mit cos(n*pi) werden die Spezialwerte +1 und -1 addressiert. Darum ist folgende Ersetzung erlaubt.
Und wer mit negativen Vorzeichen sparen will, darf auch schreiben:
Für Deine Fourierreihe bedeutet das, dass alle Koeffizienten mit geraden Zählern n verschwinden. Und alle Koffizienten mit ungeraden Zähler nehmen den Wert 1- (-1) = 2 an. Ganz zum Schluss verbleibt
für alle ungeraden Koeffizienten und 0 für alle geraden.