Ableitungen zeichnen?
Hi,
Gibt es eine feste Regel wie man sich so etwas merken kann. Also z.b. das wenn man eine Funktion hat die wie ein W verläuft die Ableitung immer wie ein N verläuft.
Kann man so etwas auch für Geraden,Parabel etc. sagen? Ich weiß nämlich nie wenn ich eine Funktion habe wie die Ableitung ungefähr aussehen muss. Oder wenn zwei gegeben sind welche der beiden jetzt die Ableitung ist und welche die ursprüngliche.
4 Antworten
Statt sich "alle möglichen" Muster merken zu wollen ist es sicher besser/einfacher/weniger umfangreich sich die Beziehungen zwischen Funktion und ihrer Ableitung an markanten Punkten zu merken/klar zu machen. Es gibt ja z. B. nicht nur Polynomfunktionen, sondern auch gebrochen-rationale, trigonometrische, Exponentialfunktionen, ... So kann z. B. auch der Ausschnitt einer Sinusfunktion einem w ähneln; die Ableitung aber auch (cos), nur u. a. etwas verschoben.
Du weißt sicher, dass die Ableitung die Steigung einer Funktion angibt:
- bei Extremstellen ist die Steigung einer Funktion Null, d. h. dort hat die Ableitung eine Nullstelle
- an Wendestellen ist die Steigung einer Funktion maximal, d. h. dort hat die Ableitung eine Extremstelle
- sinkt der Funktionsgraph, muss der Ableitungsgraph unterhalb der x-Achse verlaufen; bei steigendem Funktionsgraph entsprechend oberhalb der x-Achse
Die Ableitung sieht immer weniger kompliziert aus wie die Ursprungsfunktion. Weil sie ein Grad niedriger ist.
man braucht einfach Beispiele zum üben
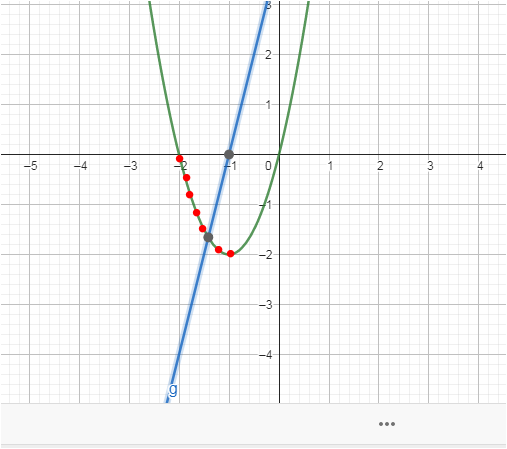
zur Parabel ist die Ableitung immer eine Gerade
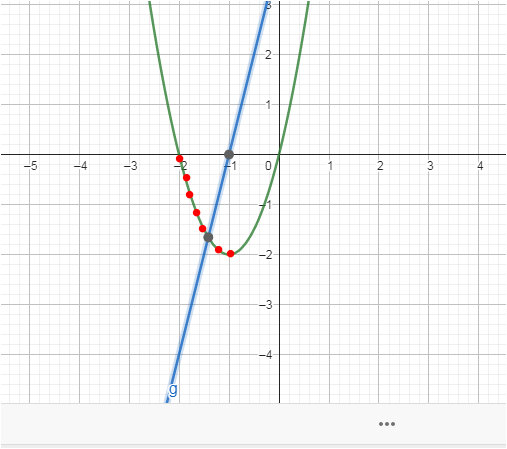
da hat die Par eine negative Steigung . Wo ist die Gerade und warm schneidet sie die x - Achse dort ?
.
.
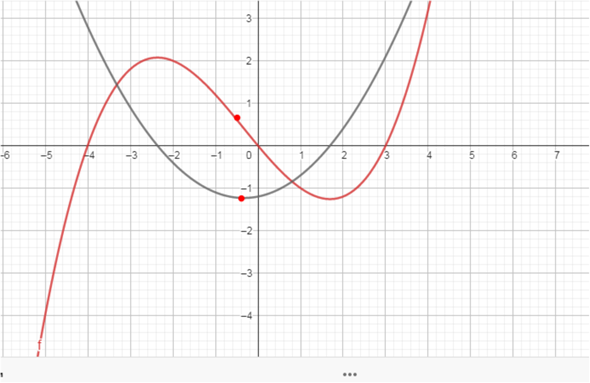
für x³ immer eine Parabel
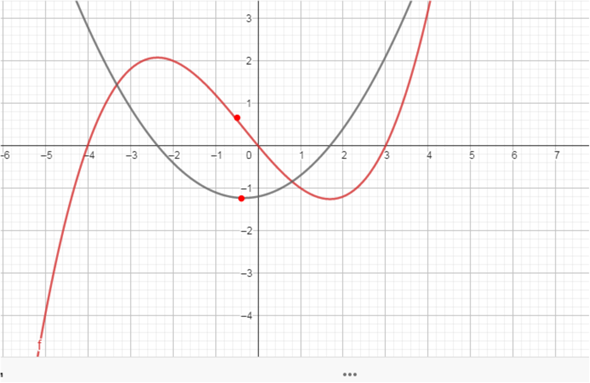
beachte nun auch die beiden roten Punkte . Was ist der bei x³ , was bei x²
Wenn du den Grad der Funktion erkennen kannst, kannst du dir ne Faustregel machen, dass der Ableitungsgraph halt den Grad=Grad-1 har