Kann mir jemand bei der aufgabe helfen bitte
danke im voraus
Gegeben:
σₐ = 20,0 N/mm²
σ꜀ = 50,0 N/mm²
τᴮ = 80,0 N/mm²
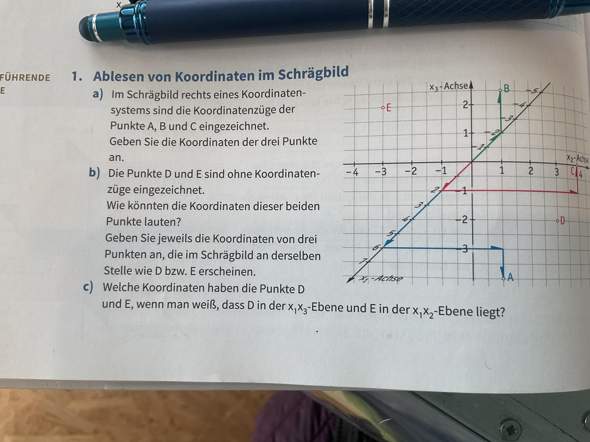
Aus dem Dreieck (Grafik):
a = 4 Kästchen (x-Richtung)
b = 3 Kästchen (y-Richtung)
l = √(a² + b²) = √(4² + 3²) = √(16 + 9) = √25 = 5
a) Gesuchte Größen: τₐ, τ꜀, σᴮ
1. τₐ:
τₐ = (a · τᴮ + b · σᴮ) / l
τₐ = (4·80 + 3·80) / 5 = (320 + 240) / 5 = 560 / 5 = 112,00 N/mm²
2. τ꜀:
τ꜀ = (a · σₐ + b · τₐ) / l
τ꜀ = (4·20 + 3·112) / 5 = (80 + 336) / 5 = 416 / 5 = 83,20 N/mm²
3. σᴮ:
σᴮ = (−b · σₐ + a · τₐ) / l
σᴮ = (−3·20 + 4·112) / 5 = (−60 + 448) / 5 = 388 / 5 = 77,60 N/mm²
b) Hauptschubspannung τₘₐₓ und zugehörige Normalspannung σᴹ
1. τₘₐₓ:
τₘₐₓ = ½ · √[(σ꜀ − σₐ)² + 4 · τ꜀²]
τₘₐₓ = ½ · √[(50 − 20)² + 4·(83,2)²]
= ½ · √[900 + 4·6928,64]
= ½ · √[900 + 27714,56]
= ½ · √28614,56
= ½ · 169,06
= 84,53 N/mm²
2. σᴹ:
σᴹ = (σₐ + σ꜀) / 2 = (20 + 50) / 2 = 35,00 N/mm²
Ergebnisse:
Teil a)
τₐ = 112,00 N/mm²
τ꜀ = 83,20 N/mm²
σᴮ = 77,60 N/mm²
Teil b)
τₘₐₓ = 84,53 N/mm²
σᴹ = 35,00 N/mm²