Wie bestimmt man die Höhe eines Dreiecks, wenn drei Punkte im dreidimensionalen Raum gegeben sind?
Sonst habe ich immer den Mittelpunkt der Grundseite berechnet und mit den anderen punkt verbunden und den betrag gebildet. Das geht aber nicht immer
3 Antworten
Mit dem Lotfußpunktverfahren müsste es eigentlich immer gehen.
Ergänzung:
Nehmen wir an, es sind gegeben:
A(0|2|3), B(3|2|1), C(2|2|5)
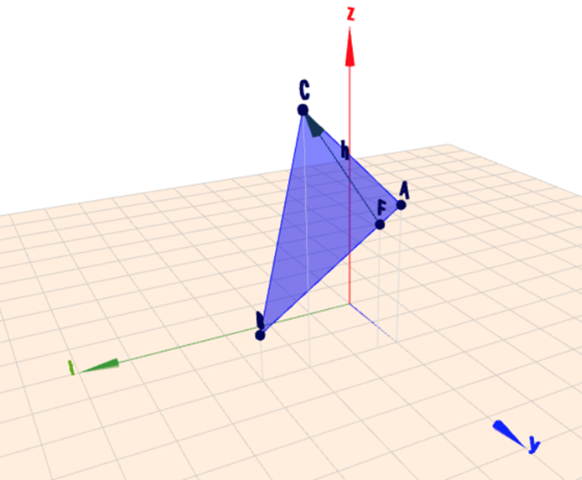
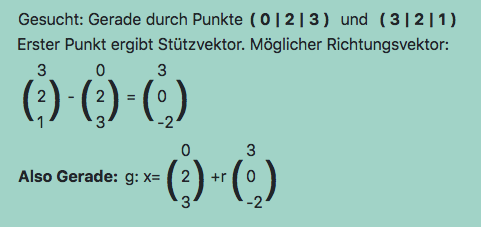
Dann ist die Gerade durch A und B:
Nun bestimmen wir die Hilfsebene H, die senkrecht zu g liegt und den Punkt C enthält. Die Koordinaten dieser Hilfsebene entsprechen den Koordinaten des Richtungsvektors von g:
H: 3x + 0y -2z = s
s bestimmmen wir, indem wir die Koordinaten von C einsetzen:
3*2 + 0*2 -2*5 = -4
s = -4
Damit lautet die Hilfsebene:
H: 3x - 2z = -4
Nun bestimmen wir den Schnittpunkt von H mit g, indem wir die Koordinaten von g in H einsetzen:
3(0 + 3r) + 0(2 + 0r) - 2(3 - 2r) = -4
und lösen nach r auf:
9r - 6 + 4r = -4
13r - 2 = 0
r = 2/13 (bei Klausuraufgaben kommt da wahrscheinlich ein glatter Wert raus)
Mit r können wir nun aus der Geraden den Schnittpunkt berechnen und das ist gleichzeitig der Lotfußpunkt F:
F: (0 + 2/13 * 3 | + 2 + 0 / 3 | 3 - 2 * 2/13) = (6/13 | 2 | 35/13)
Nun bilden wird den Vektor FC:
FC = C - F = (1,54 / 0 / 2,31)
und der hat den Betrag h = 2,7735
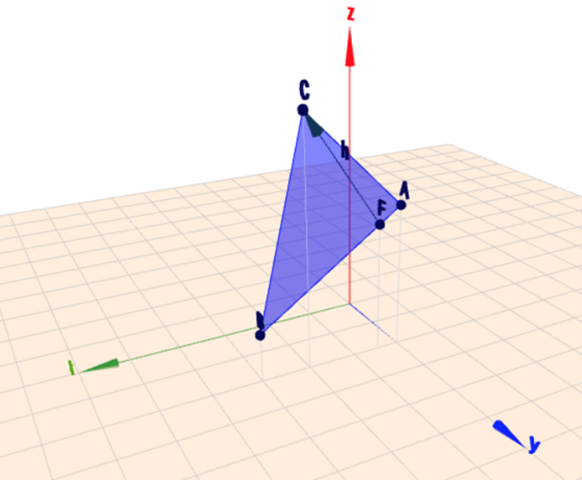
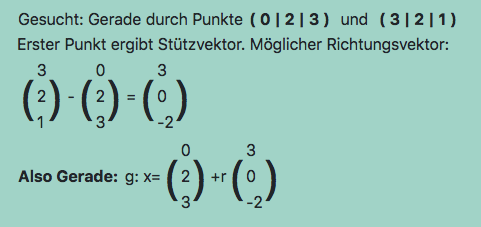
Mit Hilfe des Skalarproduktes kannst du den Fußpunkt F der Höhe bestimmen.
Der Betrag des Vektors F zu Spitze des Dreiecks ist die gesuchte Höhe.
Hallo,
Höhe mal halbe Grundseite ergibt die Fläche des Dreiecks.
Die Fläche ist aber auch der halbe Betrag des Kreuzproduktes.
Wenn Du also die Fläche hast und den Betrag der Grundseite, ist es leicht, daraus den Betrag der Höhe zu bestimmen.
Das Kreuzprodukt zweier Verbindungsvektoren von jeweils zwei Punkten des Dreiecks. Einer der Vektoren ist dann die Grundseite.
Herzliche Grüße,
Willy
Also wenn ich ein Dreieck ABC habe und AB die Grundseite ist, stelle ich eine Gerade auf, die durch AB geht und verbinde den allgemeinen Punkt der Geraden mit C und bilde das Skalarprodukt mit den AB vektor. Ist das richtig?