Wie berechnet man die höhe eines Dreiecks wenn alle seiten gegeben sind?

Man kann die Höhe wie folgt berechnen, wenn die 3 Seiten gegeben sind.
Nachfolgend ein Beispiel.

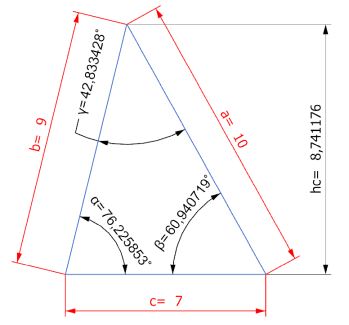
z.B. Berechnung der Höhe hc wie folgt:

α= ARCCOS( (a² - b2 - c²) / (-2 * b * c) )
α= ARCCOS( (10² - 9² - 7²) / (-2 * 9 * 76,22585) )
α = 76,225853001973°

β = ARCCOS( (b² - a² - c²) / (-2 * a * c) )
β = ARCCOS( (9² - 10² - 7²) / (-2 * 10 * 7) )
β = 60,940718931960°

γ = 180 - α - β
γ = 180 - 76,22585 - 60,94072
γ = 42,833428066067°

hc = a * SIN(β)
hc = 10 * SIN(60,940719)
hc = 8,741176

Die Holzhammer-Methode ist die Heronsche Formel. Dann hat man aus den drei Seiten sofort den Flächeninhalt A.

Dann sucht man sich eine Seite s aus und kann über A = s * h / 2 die entsprechende Höhe ausrechnen.

Hinweis: Die Heronsche Formel benutzt man nur dann, wenn einem wirklich nichts besseres einfällt.

es gibt drei Höhen ............aber auch ich will die Höhe auf c , hc und nenne sie hier h

AF nenne ich x und AB ist selbstverständlich c

b² = h² + x²........(1)
...................................a² = h² + (c-x)²........................(2)

zwei Glg mit zwei Unbekannten ist locker machbar (*****)

denn man macht aus (1) .............. x² = b² - h² bzw x = wurz(b² - h²) und setzt das in (2) nach dem Ausmultiplizieren ein

a² = h² + c² - 2*c*wurz(b² - h²) + (b² - h²) ............h² fällt weg
a² = c² - 2*c*wurz(b² - h²) + b²
nun geht der Spaß erst richtig los ............alle außer dem Term mit Wurzel nach links und dann Quadrieren

a² - c² - b² = - 2*c*wurz(b² - h²)
=
( a² - c² - b² )² = 4c² * (b² - h²)....... nun durch 4c² und danach -b² und mal -1
[ ( a² - c² - b² )² / 4c² - b² ] * (-1) und nun draus die Wurzel

(*****) locker ist was anderes , die Hölle ist es nicht , aber schön auch nicht .

Viel Spaß .............Tipp , nimm ein gleichschenkeliges Dreieck , dann ergibt a²-b² Null :))