Wie bestimmt man den Grenzwert dieser Folge?

Answer 1

[mihisu]

Bei solchen Aufgaben hilft es oftmals die höchste Potenz der Variable (hier n) bei Zähler und Nenner auszuklammern, und dann zu schauen, inwieweit man kürzen kann. [Dies hat den Sinn, dass man danach hauptsächlich noch Terme wie 1/n, 1/n², ... stehen hat, die gegen 0 konvergieren. Und dann hat man mit dem, was noch übrig bleibt, schnell den Grenzwert gefunden.]

Answer 2

[Halbrecht]

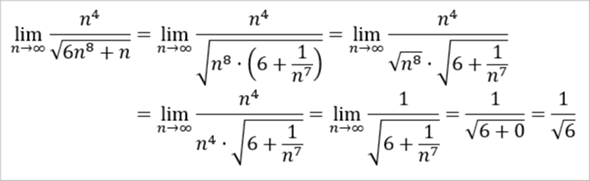
wir zaubern aus n hoch 4

wurz(n hoch 8)

Kürzen den Bruch mit wurz( n hoch 8)

bleibt

1 / ( wurz(6 + 1/n hoch 7) ) 

wenn n nun gegen unend geht (egal ob + oder -)

dann wird der Bruch 1/n hoch 7 vernachlässigbar klein

und es bleibt

1 / wurz(6) als Grenzwert

Answer 3

[Willy1729]

Hallo,

da das Zählerpolynom einen höheren Grad hat als der Nenner, geht die Folge gegen unendlich.

n^4 wächst wesentlich schneller als die Wurzel aus (6n^3+n).

Herzliche Grüße,

Willy

Comments

[Loyaltinesswess]

(6n^8+n)*

[Willy1729]

@Loyaltinesswess

Ich hatte unter der Wurzel 6*n^3 gelesen.

Wenn es 6*n^8 heißt, ist der Grenzwert natürlich 1/Wurzel (6).

Answer 4

[nobytree2]

$\lim_{n\to\infty\ }\frac{n^4}{\sqrt{6n^8+n}}=\frac{n^4}{\sqrt{n^8\cdot\left(6+\frac{1}{n^7}\right)}}=\frac{n^4}{\sqrt{n^8}\cdot\sqrt{6+\frac{1}{n^7}}}$ $=\lim_{n\to\infty}\frac{n^4}{n^4\cdot\sqrt{6+\frac{1}{n^7}}}=\lim_{n\to\infty}\frac{n^4}{n^4}\cdot\lim_{n\to\infty}\frac{1}{\sqrt{6+\frac{1}{n^7}}}$ $=\lim_{n\to\infty}1\cdot\left(\frac{1}{\sqrt{6+\frac{1}{\lim_{n\to\infty}n^7}}}\right)\to\frac{1}{\sqrt{6+0}}=6^{-\frac{1}{2}}$

also 1 durch Wurzel 6. aber Vorsicht, ich verrechne mich häufig. Dann hätte ich in der ersten Zeile immer noch Limes wiederholen müssen.

Comments

[Halbrecht]

alles gut , Hauptsache wir sehen ,dass um halb Sechs die Grenze erreicht ist !

Answer 5

[DerRoll]

Zähler und Nenner durch n^4 teilen, dann die Wurzelgesetze ausnutzen und damit das n^4 als n^8 in einen Nenner unter die Wurzel ziehen.

Woher ich das weiß: Studium / Ausbildung – Dipl.Math.

Comments

[Halbrecht]

Rasenball Leibzisch wird heut eine HimbeerWurzelbehandlung beim anwenden. Taschentücher bereithalten .