Wie berechnet man die Ableitung?
3 Antworten
wie nennen ?
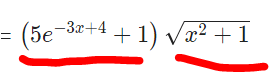
u und v wie oben
u ' = -3x * 5e^(-3x+4)
v' = 1/2 * 2x * (x² + 1)^(-1/2)
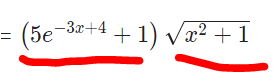
die einen so , die anderen so .
wikipedia verwendet auch die Kurze Version ( u*v )'
Habe oben eine längere Antwort geschrieben. Wäre das so richtig?
Wie bekomme ich denn die 1 weg, wenn ich das so aufschreibe? Wo verschwindet sie genau?
Mit der Produktregel und Kettenregel. 5e^-3x+4 +1 ist u und Wurzel aus x^2 + 1 ist v.
Jetzt bildest du von u und v einzeln die Ableitungen und packst alles in diese Formel rein: f'(x) = u' × v + u × v'. Das ist schon die Ableitung, aber sie wird ziemlich unordentlich aussehen, wenn du sie so lässt. Du könntest den e-Term ausklammern.
Um den u Teil mit der e-Funktion abzuleiten, brauchst du die Kettenregel. Das ist einfach die Ableitung des Exponenten mal den ganzen e-Term. Hier: 5e^-3x+4 × (-3) = -15e^-3x+4
Ich frage mich irgendwie nur, wie ich die einzelnen Funktionen immer nennen soll. Das verwirrt mich voll.
Meinst du die Bestimmung von u und v? Im Grunde ist egal, was von beiden u und v ist. Ich hätte auch sagen können, dass der e-Term v ist und der Wurzelterm u. Du musst nur darauf achten, dass der *gesamte* Teil vor dem Malzeichen z. B. u ist und der restliche nach dem Mal dann v (oder andersrum). Bei 3x × 12x^4 + 7 beispielsweise ist also der erste gesamte Teil vor dem × die 3x. Das können wir u nennen. Der restliche Teil nach dem × ist 12x^4 + 7, das ist dann v.
Sagen wir mal ich nenne den e-Term u(x) und den Wurzelterm v(x).
Ich muss ja den e-Term weiter aufteilen in die äußere- und innere Funktion (Kettenregel), die ich beide auch nochmal wiederum benennen muss.
Dann wäre u(x) der erste Teil, v(x) wäre die äußere Funktion (also 5e^(-3x+4) + 1) und w(x) wäre die innere Funktion (also -3x+1).
Dann:
v'(x)=5e^(-3x+4)
w'(x)=-3
u'(x)=v'(w(x)) * w'(x) = 5e^(-3x+4) * -3 = -15e^(-3x+4)
Oder?
wieso liest du nicht meine Antwort , da steht es doch
.
Und du kannst die + 1 nicht einfach weglassen . In der Ableitung verschwindet sie zwar und nicht in u !
Ich würde es so aufschreiben:
u(x) = 5e^x
v(x) = -3x + 4
v'(x) = -3
Dann in die Formel einsetzen, wobei ich dieses kleinschrittige und die Formel für die Kettenregel mühsam/irritierend finde. Merk dir für die Ableitung der e-Funktion einfach den gesamten e-Term mit der Ableitung des Exponenten multiplizieren.
Du hast die Kettenregel richtig angewendet, aber ziemlich verwirrend aufgeschrieben. Und hast auch das hier geschrieben: v'(x)=5e^(-3x+4). Pass auf, weil das ist noch nicht die Ableitung, also statt v'(x) ist das noch v(x)
Ah okay, aber @Halbrecht hat daran erinnert, dass u(x) = 5e^x + 1 wäre
Ja, bei der Produktregel auf jeden Fall. Er/sie meint aber die Ableitung des e-Terms mit der Kettenregel. Da entfällt die + 1 beim Ableiten sowieso
kann man , aber wo bleibt die +1 ??????
Komplett sieht das Ganze so aus u v' * u' v =
(5e^(-3x+4) + 1 ) mal (x² + 1) plus ( -3x * 5e^(-3x+4) ) * ( 1/2 * 2x * (x² + 1)^(-1/2) )
mit Produkt- und Kettenregel
hilfreich kann sein:
https://www.ableitungsrechner.net/
da kann man sich auch den Rechenweg anzeigen lassen
Wieso nicht u'(x) und v'(x) ?