Wie berechnet man die n-te Ableitung von f?
Hallo! Ich wollte Fragen, ob jemand weiß, wie man die n-te Ableitung von f berechnet. Also jetzt nicht nur die 5-te Ableitung, sonder z.B. die 1.25-te Ableitung. Geht das überhaupt. Ich habe gehört, dass die 0,5-te Ableitung geht, aber die 1, Periode 3-te Ableitung? Oder die 3-7i-te Ableitung? Gibt es eine Formel für die n-te Ableitung, wenn n Element von C ist? Und wenn ja, welche?
3 Antworten
Hallo!
Hallöchen!
Ich wollte Fragen, ob jemand weiß, wie man die n-te Ableitung von f berechnet.
So eine gibt es nicht.
Einerseits ist das mit "der einen Formel" schwer, anderer Seitz verschwimmen dabei Integralrechnung und Differentialrechnen, wobei du auch bei Formeln landen kannst die nicht in eine geschlossene Form gebracht werden können.
Das muss man in der Regel für alle f einzeln herrausfinden.
Geht das überhaupt. Geht das überhaupt. Ich habe gehört, dass die 0,5-te Ableitung geht, aber die 1, Periode 3-te Ableitung? Oder die 3-7i-te Ableitung?
Das geht. Das ist ein eigener Teilbereich der Mathematik, welcher Fraktionale Infinitesimalrechnung (besser bekannt als fractional calculus)m, was ich in folgenden als FIR bezeichnen werde da die Wörter so unnötig lang sind, genannt wird. Da können wir jede Ableitung ziehen von allem was wir wollen.
Auch die 2 + 8i-te Ableitung (ja man kann auch 2 + 8i mal ableiten (Beispiele: i-te Ableitung von x^i und i-te Ableitung von x) oder x-mal Ableiten.
Du kannst aber auch negative Ableitungen berechnen, z.B. die -1-Ableitung, welche gemäß des Fundamentalsatz der Analysis (F'(x) = f(x)) das erste Integral ist:
Ich wollte Fragen, ob jemand weiß, wie man die n-te Ableitung von f berechnet.
Jetzt kommen wir direkt zu einer eigenartigen der FIR:
- Ähnlich wie du es von Integralen kennst gibt es hier nicht mehr "die eine Ableitung", sondern unendlich viele.
- FIR ist in der Regel nur eine Verallgemeinerung von der IR, wobei die Regel die für IR Mittels der Beziehung zu speziellen Funktionen erweitert werden, weswegen FIR in der Regel ein enormes Verständnis von speziellen Funktionen erfordert, wie z.B. von der Gammafunktion, den hypergeometrischen Funktionen, ...
Ein klassisches Beispiel dafür ist die e-Funktion:
Beispiel e-Funktion
klassisch:
D exp(a * x) = a * exp(a * x)
D² exp(a * x) = a² * exp(a * x)
D³ exp(a * x) = a³ * exp(a * x)
-> wir erkennen das Muster D^n exp(a * x) = a^n * exp(a * x)
Sagen wir, dass das für alle n gilt dann können wir sagen:
D^i exp(a * x) = a^i * exp(a * x)
aka die i-te Ableitung aus exp(ax) ist a^i * exp(ax).
Wir können aber auch anders argumentieren:
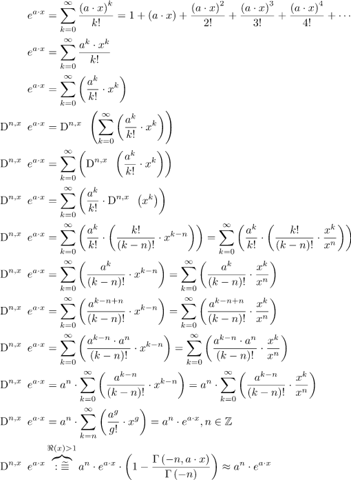
in LaTeX:
\begin{align*}
e^{a \cdot x} &= \sum_{k = 0}^{\infty} \frac{\left( a \cdot x \right)^{k}}{k!} = 1 + \left( a \cdot x \right) + \frac{\left( a \cdot x \right)^{2}}{2!} + \frac{\left( a \cdot x \right)^{3}}{3!} + \frac{\left( a \cdot x \right)^{4}}{4!} + \cdots\\
e^{a \cdot x} &= \sum_{k = 0}^{\infty} \frac{a^{k} \cdot x^{k}}{k!}\\
e^{a \cdot x} &= \sum_{k = 0}^{\infty} \left( \frac{a^{k}}{k!} \cdot x^{k} \right)\\
\operatorname{D}^{n, x}~ e^{a \cdot x} &= \operatorname{D}^{n, x}~ \left( \sum_{k = 0}^{\infty} \left( \frac{a^{k}}{k!} \cdot x^{k} \right) \right)\\
\operatorname{D}^{n, x}~ e^{a \cdot x} &= \sum_{k = 0}^{\infty} \left( \operatorname{D}^{n, x}~ \left( \frac{a^{k}}{k!} \cdot x^{k} \right) \right)\\
\operatorname{D}^{n, x}~ e^{a \cdot x} &= \sum_{k = 0}^{\infty} \left( \frac{a^{k}}{k!} \cdot \operatorname{D}^{n, x}~ \left( x^{k} \right) \right)\\
\operatorname{D}^{n, x}~ e^{a \cdot x} &= \sum_{k = 0}^{\infty} \left( \frac{a^{k}}{k!} \cdot \left( \frac{k!}{\left( k - n \right)!} \cdot x^{k - n} \right) \right) = \sum_{k = 0}^{\infty} \left( \frac{a^{k}}{k!} \cdot \left( \frac{k!}{\left( k - n \right)!} \cdot \frac{x^{k}}{x^{n}} \right) \right)\\
\operatorname{D}^{n, x}~ e^{a \cdot x} &= \sum_{k = 0}^{\infty} \left( \frac{a^{k}}{\left( k - n \right)!} \cdot x^{k - n} \right) = \sum_{k = 0}^{\infty} \left( \frac{a^{k}}{\left( k - n \right)!} \cdot \frac{x^{k}}{x^{n}} \right)\\
\operatorname{D}^{n, x}~ e^{a \cdot x} &= \sum_{k = 0}^{\infty} \left( \frac{a^{k - n + n}}{\left( k - n \right)!} \cdot x^{k - n} \right) = \sum_{k = 0}^{\infty} \left( \frac{a^{k - n + n}}{\left( k - n \right)!} \cdot \frac{x^{k}}{x^{n}} \right)\\
\operatorname{D}^{n, x}~ e^{a \cdot x} &= \sum_{k = 0}^{\infty} \left( \frac{a^{k - n} \cdot a^{n}}{\left( k - n \right)!} \cdot x^{k - n} \right) = \sum_{k = 0}^{\infty} \left( \frac{a^{k - n} \cdot a^{n}}{\left( k - n \right)!} \cdot \frac{x^{k}}{x^{n}} \right)\\
\operatorname{D}^{n, x}~ e^{a \cdot x} &= a^{n} \cdot \sum_{k = 0}^{\infty} \left( \frac{a^{k - n}}{\left( k - n \right)!} \cdot x^{k - n} \right) = a^{n} \cdot \sum_{k = 0}^{\infty} \left( \frac{a^{k - n}}{\left( k - n \right)!} \cdot \frac{x^{k}}{x^{n}} \right)\\
\operatorname{D}^{n, x}~ e^{a \cdot x} &= a^{n} \cdot \sum_{k = n}^{\infty} \left( \frac{a^{g}}{g!} \cdot x^{g} \right) = a^{n} \cdot e^{a \cdot x}, n \in \mathbb{Z}\\
\operatorname{D}^{n, x}~ e^{a \cdot x} &\overbrace{:\widetilde{\equiv}}^{\Re\left( x \right) > 1} a^{n} \cdot e^{a \cdot x} \cdot \left( 1 - \frac{\Gamma\left( -n, a \cdot x \right)}{\Gamma\left( -n \right)} \right) \approx a^{n} \cdot e^{a \cdot x}\\
\end{align*}
Die beiden Ausdrücke sind ganz klar nicht gleich, jedoch sind sie beide zu 100% richtig hergeleitet.
Gibt es eine Formel für die n-te Ableitung, wenn n Element von C ist? Und wenn ja, welche?
Nein. musst du dir selbst herleiten für jede Funktion einzeln herleiten.
Persönliche Tipps- Wenn du dich weiter mit FIR beschäftigen willst, solltest du dich darauf einstellen, dass du oft nur Artikel und Arbeiten in englisch findest.
- Da fast alles in FIR auf speziellen Funktionen beruht, sollte man sich davor wenigstens die Basics dazu und die wichtigsten speziellen Funktionen dafür anschauen (aka die Gammafunktion, Betafunktion und hypergeometrische Funktionen).
- Wenn du dich dafür interessierst könntest du auch untersuchen, was die x-te Ableitung von f(x) ist. Sehr cooles Thema und die Funktionen sehen dabei in der Regel recht schön aus. ;)
- Bei weiteren Fragen dazu kannst du gerne auf GF fragen, oder auch mich, da das eines meiner drei Lieblingsthemen in der Mathematik ist. :)
Noch Fragen? x)
Es gibt einige interessante Verallgemeinerungen der Ableitung wie die auf rationale Ableitungsexponenten. Das ist dann aber eher Freizeitmathematik ohne wirklichen akademischen Nutzen.
Hier findest du ein Video dazu:
Das werde ich auch meiner Sammlung hinzufügen. :lol:
Wenn du dich für Fraktionale Infinitesimalrechnung interessierst, könntest du dir ja mal anschauen was passiert, wenn du eine Funktion f(x) x mal Ableitest, also
d^x/dx^x f(x)
Dabei kommen in der Regel echt coole und unerwartete Graphen raus.
Beispiele:
d^x/dx^x x^m = \frac{m!}{\left(m-x!\right)}\cdot\frac{x^{m}}{x^{x}}
Dich könnten dann auch die Untersuchung von speziellen Funktionen damit interessieren. :3
Das ganze würde ich dann einfach unter weiterer "[...] Freizeitmathematik ohne wirklichen akademischen Nutzen." abtun. :rofl:
Vielen Dank! Ich mag Freizeitmathematik sehr gerne. Ich brauche das auch alles noch gar nicht. Ich lerne eine normale Ableitung in der Schule in 3 Jahren.
Der Begriff der Ableitung ist nach meinem Kenntnisstand nur für n € Z definiert (für negative n über den Hauptsatz der Differential- und Integralrechnung).
Nicht ganzzahlige Werte für n machen insbesondere deshalb keinen Sinn, weil der Begriff der n-ten Ableitung rekursiv definiert ist.
Schade! Ich habe nämlich schon oft etwas von der 0,5-ten Ableitung gehört.
Wieder was gelernt von dir. Wobei der Begriff "Freizeitmathematik ohne wirklichen akademischen Nutzen" eine ganz besondere Position in meiner Sammlung von zitierfähigen Begriffen bekommen wird :rofl: