Wertemenge bestimmen?Einfache gebrochen-rationale Funktion?
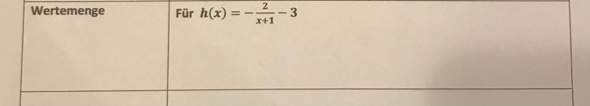
Wie bestimmt man die Wertemenge von h(x)?
Wertemenge:
-> Alle y-Werte, die bei einer Funktion rauskommen können
Mit dieser Definition kann ich leider nichts anfangen. Kann mir das bitte jemand einfach erklären? Ich bin schon am Verzweifeln :(
Danke
3 Antworten
Gemeint ist wahrscheinlich, dass Du die Menge aller möglichen y-Werte allgemein darstellst, und Dir dabei überlegst, wo die Funktion nicht definiert ist und ob es für x einen Grenzwert gibt, wenn x gegen minus oder plus unendlich strebt.
Was man sofort sagen kann, ist, dass die Funktion bei x= -1 nicht definiert ist, weil dort dann der Nenner des Bruchs null wird, und Divsion durch null ist bekanntlich nicht definiert.
Dann stellt sich noch die Frage, wie es mit den Grenzwerten aussieht:
Berechnest Du den Grenzwert (Limes) wenn x gegen unendlich strebt, erhältst Du -3.
Für minus unendlich ist es ebenfalls -3.
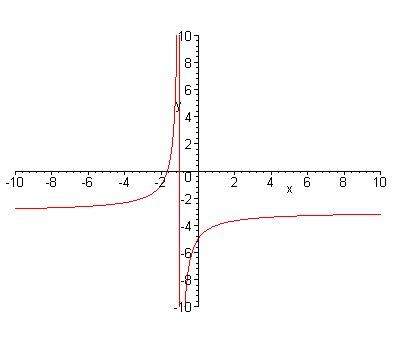
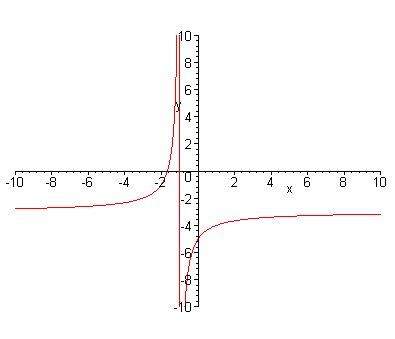
Das heisst: für alle x > -1 liegen die y-Werte zwischen -3 und und minus unendlich,
für alle x < -1 liegen die y-Werte zwischen -3 und plus unendlich.
An die Wertemenge kommt man, indem man die Extremstellen ermittelt (falls vorhanden), dazu die Grenzwerte an Definitionslücke(n) und im ±-Unendlichen.
Aus den Ergebnissen daraus wird man den Wertebereich bestimmen können (evtl. den Graphen skizzieren, um sich die berechneten Ergebnisse besser vorstellen zu können).
Eine andere Möglichkeit wäre die Ermittlung der Umkehrfunktion (falls möglich). Der Definitionsbereich der Umkehrfunktion ist der Wertebereich der Ausgangsfunktion.
Hier noch der Funktionsgraph für's besser Verständnis. Die vertikale rote Linie gehört nicht zum Graph, sondern ist ein Zeichnungsfehler des Grafikprogramms.