Was ist der Unterschied zwischen Drachen und symetriedrachen?
. ich weiss nicht ob überhaupt einen Unterschied gibt.Iche weiss ein Drachen ist eine spezielles Viereck und Rauter ist ein spezielles Drachen. Aber im Buch gibt es zwei Zeichnungen-> Drachen und symmetrie Drachen.Wie kann ein Drachen NICHT symmetrie sein?
5 Antworten
Wie ist in der Mathematik der Begriff "Drache" definiert"? Ein Drachenviereck ist ein Viereck, bei dem eine Diagonale die andere Diagonale halbiert.
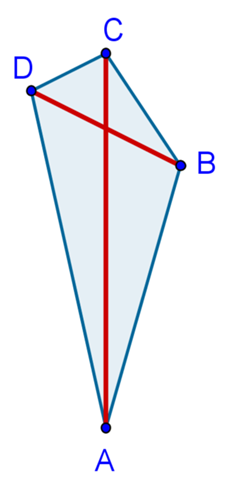
Also kann ein Drachen auch so aussehen (siehe unten):
Hier teilt AC die Digonale BD genau in der Mitte.
Schließen die Diagonalen einen rechten Winkel ein (so wie man sich einen Drachen vorstellt), erhält man einen symmetrischen Drachen.

Also KDwalther, wie das Buch sagt , es gibt normales Drachen und dann spezifisch Drachen, we symmetriedrachen und Rauter. wichtig jetzt klar ,dass ei bei Rauter muss nicht jede nachbarseite gleich lang wie bei symmetirie Drachen.das wollte ich das wissen.. das heisst wenn ein Viereck, bei dem eine Diagonale die andere Diagonale halbiert.ist dann erstmal ein Drachen und muss nicht unbedingt symmetrisch. das ist genau was ich wissen wollte
Das ist ja häufig so, dass ein bestimmter Begriff sowohl in der Mathematik als auch im "täglichen Leben" vorkommt, nur dass die Bedeutung/Definition unterschiedlich sein können.
So heißt im Leben z.B. "Steigung": es geht nach oben.
In der Mathematik wird damit eher der Winkel zur Waagerechten ausgedrückt; daher gibt es auch eine negative Steigung oder die "Steigung" null ;-)
Hast du mal ein Foto von den Abbildungen? Ich kann mir darunter nämlich auch gerade nichts vorstellen.
Du weißt ja anscheinend auch, dass bei Drachenvierecken immer eine Diagonale Symmetrieachse ist. Wenn die zweite Diagonale auch Symmetrieachse ist, spricht man von einer Raute.
Anscheinend kann man sich darüber streiten , besser nicht einer Meinung sein :
wikipedia definiert den "'eigentlichen" Drachen als den Symmetriedrachen und führt dann den auf :
Ein schräges Drachenviereck ist ein ebenes Viereck, in dem eine der Diagonalen durch die andere halbiert wird.[2] (Ein solches Viereck wird manchmal auch 'schief' genannt.[3]) Bei einem schrägen Drachenviereck stehen die Diagonalen also nicht zwangsläufig orthogonal zu einander. Das Deltoid ist in diesem Sinne ein gerader Drachen. Für das schräge Drachenviereck gilt eine über das Kreuzprodukt verallgemeinerte Formel für den Flächeninhalt.
https://de.wikipedia.org/wiki/Drachenviereck
interessant dabei : Nun wird das PARALLELOGRAMM zum schiefen Drachen


Meinst du nicht, dass es gerade in diesem Fall
sinnvoll wäre, die Abbildungen zu zeigen?
Ein Drachenviereck ist normalerweise ein
Viereck mit einer Symmetrieachse, d. h.
zwei Winkel sind gleich und je zwei Seiten
sind paarweise gleich.
Eine Raute ist ein Viereck mit vier gleichlangen Seiten.
Man müsste jetzt sehen, was euer Buch darunter versteht.
wie im Buch steht : es gibt ein Drachen und symmtriedrachen.ich dachte am Anfang jede drachen muss symmetrisch sein aber jetzt ist klar .
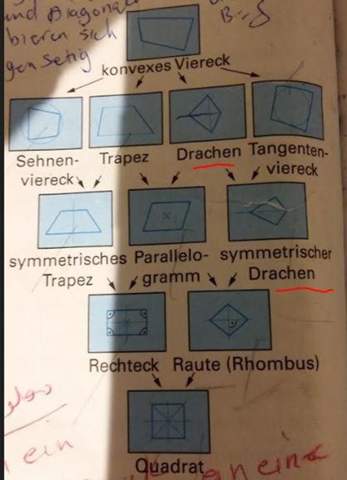

......