Wie bestimmt man C und D damit ABCD eine Raute ist?
Die Fragestellung lautet: „Bestimmen Sie mögliche Punkte C und D so, dass das Viereck ABCD eine Raute ist.“
Ich habe A(1|2|3|) und B(-2|-1|-3) und dadurch auch den Mittelpunkt von der Strecke AB. Die Lösung in meinem Buch sagt, dass D(4|-4|0) und C(1|-7|-6) sein könnte, aber ich weiß nicht, wie ich das rausbekomme.
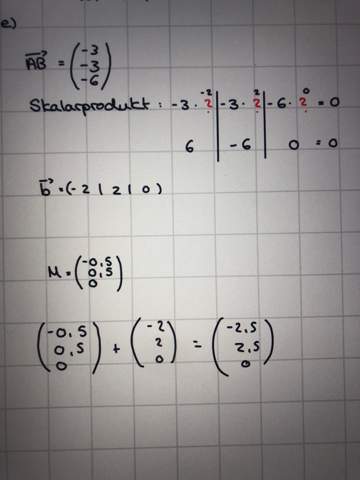
So weit bin ich gekommen
3 Antworten
Bei der Aufgabenstellung gibt es mehere Lösungen, weshalb ja auch die Wörter "möglich" und "könnte" in der Aufgabe vorkommen. Welcher Lösungsweg auf die Musterlösung führt, weiß ich nicht. Ich würde jedenfalls so vorgehen:
Zum Finden von C und D benutze ich die Eigenschaft, dass alle Seiten gleichlang und parallel sein müssen. Die Eigenschaft, dass die Diagonalen senkrecht aufeinander stehen, verwende ich dann zur Probe.
Zuerst berechne ich den Vektor AB:
AB = B - A = (-2/-1/-3) - (1/2/3) = (-3/-3/-6)
Dieser Vektor hat die Länge:
⎜AB⎜ = √(-3)^2 + (-3)^2 + (-6)^2 = √54
Ansatz für C:
C(x1/x2/x3)
Damit ergibt sich ein Vektor BC:
BC = C - B = ((x1+2) / (x2 + 1) / (x3 + 3)
Und der hat die Länge:
⎜BC⎜ = √((x1+2)^2 + (x2 + 1)^2 + (x3 + 3)^2)
Da ⎜AB⎜ = ⎜BC⎜ sein muss, gilt also:
√((x1+2)^2 + (x2 + 1)^2 + (x3 + 3)^2) = √54
Die 54 kann ich nun beliuebig aufteilen. Ich wähle eine Möglichkeit so, dass 54 die Summe von Quadraten ganzer Zahlen ergibt.
Eine Möglichkeit wäre:
1^1 + 2^2 + 7^2 = 54
Das müssen die Faktoren des obigen Terms √((x1+2)^2 + (x2 + 1)^2 + (x3 + 3)^2) sein. Daraus ergibt sich:
x1 + 2 = 1
x1 = -1
x2 + 1 = 2
x2 = 1
x3 + 3 = 7
x3 = 4
Damit lautet ein mögliches C:
C(-1/1/4)
Damit ergibt sich BC:
BC = C - B = (-1/1/4) - (-2/-1/-3) = (1/2/7)
Da AD und BC gleichlang und parallel sein müssen, hänge ich nun einfach BC an A ran, um so die Ortskoordinaten von D zu ermitteln:
D = A + BC = (1/2/3) + (1/2/7) = (2/4/10)
Nun mache ich vorsichtshalber die Probe:
Diagonale 1 = AC
AC = C - A = (-1/1/4) - (1/2/3) = (-2/-1/1)
Diagonale 2 = BD
BD = D - B = (2/4/10) - (-2/-1/-3) = (4/5/13)
Schneiden von AC und BD (Skalarprodukt):
AC * BD = -8 -5 + 13 = 0
Ergebnis:
Mit den möglichen Punkten C(-1/1/4) und D(2/4/10) wird zusammen mit A und B eine Raute gebildet, da alle Seiten gleich lang sowie gegenüberliegend parallel sind und die Diagonalen senkrecht aufeinander stehen.
Vielen herzlichen Dank für die genaue Antwort, das hat mir wirklich sehr geholfen!
Wenn du den Mittelpunkt der STrecke hast kannst du darauf die Senkrechte konstruieren. Denn in einer Raute schneiden sich die Diagonalen senkrecht. Dann sind alle Punkte auf der Senkrechten, die zum Mittelpunkt den jeweils gleichen Abstand haben, die fehlenden Punkte für eine Raute.
Das solltest du eigentlich im Unterricht gelernt haben. Du hast einen Vektor gegeben, nämlich die Strecke zwischen A und B. Alle Vektoren für die das Skalarprodukt mit diesem Vektor Null ergibt stehen senkrecht auf ihm. Nun mußt du noch als Aufsatzpunkt den Mittelpunkt der Strecke zwischen A und B nehmen.
Du hast eine mögliche Koordinate für einen Eckpunkt der Raute berechnet. Den zweiten erhälst du wenn du statt dessen den Vektor vom Mittelpunkt subtrahierst. Wie gesagt, mache dir eine Zeichnung in 2D, dann siehst du das besser. Ich möchte noch bemerken dass ich deine Rechnungen nicht nachvollziehe. Ich schreibe dir nur einen möglichen Lösungsweg auf.
Vier Punkte A,B,C,D bilden im Raum eine Raute, wenn folgendes gilt
(Ia)
Vektor durch A und D : v1 = (D-A) = (Dx-Ax, Dy-Ay, Dz-Az)
Vektor durch B und C : u1 = (C-B) = (Cx-Bx, Cy-By, Cz-Bz)
v1 und u1 müssen senkrecht stehen, also v1*u1 = 0
(Ib)
Vektor durch A und B : v2 = (B-A) = (Bx-Ax, By-Ay, Bz-Az)
Vektor durch C und D : u2 = (D-C) = (Dx-Cx, Dy-Cy, Dz-Cz)
v2 und u2 müssen parallel sein.
(Ic)
Vektor durch A und C : v3 = (C-A) = (Cx-Ax, Cy-Ay, Cz-Az)
Vektor durch B und D : u3 = (D-B) = (Dx-Bx, Dy-By, Dz-Bz)
v3 und u3 müssen parallel sein.
Mit (Ax,Ay,Az)=(1,2,3) und (By,By,Bz)=(-2-1,-3) müssen für C und D folgende Bedingungen erfüllt sein:
(Ia) (Dx-1)*(Cx+2) + (Dy-2)*(Cy+1) + (Dz-3)*(Cz+3) = 0
(Ib) (-3, -3, -6) = r * (Dx-Cx, Dy-Cy, Dz-Cz)
(Ic) (Cx-1, Cy-2, Cz-3) = s * (Dx-Cx, Dy-Cy, Dz-Cz)
Setzt man
(Cx,Cy,Cz) = (4,-4,0)
(Dx,Dy,Dz) = (1,-7,-6)
sind alle Bedingungen erfüllt. Somit bilden die 4 Punkte eine Raute. AB ist eine Kante und CD die parallele Gegenkante.
Setzt man
(Cx,Cy,Cz) = (4,-4,0)
Wie kommt man darauf, wenn man die Lösung noch nicht kennt?
Ok danke und wie konstruiere ich die Senkrechte?