Wie kommt man von der Normalform zur Scheitelpunktform?
Hey.
Kann mir jemand Schritt für Schritt erklären, wie ich von der Normalform zur Scheitelpunktform komme? Ich verstehe das noch nicht so ganz.
Ich muss das übrigens ohne PQ Formel, also nur mit Umrechnung und Binomischen Formeln machen.

Welche Schritte verstehst du denn nicht?
Ich hatte generell nicht verstanden was man machen muss und worauf man achten soll. Aber ich kann es jetzt. VG
3 Antworten
Die ganze Idee dabei ist: Addiere eine "0" so schlau, sodass man danach auf einen Teil des Funktionsterms eine binomische Formel anwenden kann.
Das Ganze nennt sich dann "Quadratische Ergänzung"
Und die "schlaue 0" ist immer:
wobei "b" der Faktor beim linearen Glied "x" ist (Das anfängliche Ausklammern des Steckfaktors lasse ich jetzt hier mal weg). Im Fall Deines Beispiels steht in der eckigen Klammer ein "5x" (b = 5) und damit ist zu addieren
Und schon kann man mit den ersten 3 Termen in der der eckigen Klammer die 1. binomische Formel verwenden und bekommt
PS: Dieses Vorgehen ist übrigens auch die Basis zur Herleitung von pq-Formel und Mitternachtsformel (aka: abc-Formel)
Hallo.
Such mal nach quadratischer Ergänzung. Dazu solltest du einige Videos finden, die dir genau das erklären. Es geht dabei im Grunde um das Anwenden der binomischen Formeln, nur rückwärts.
f(x) = ax² + bx + c
Als erstes klammerst du das a aus:
f(x) = a[x² + (b/a)x] + c
Daher steht bei dir nun das x² alleine und aus der 10 wurde eine 5, denn 10/2=5.
Nun halbierst du (b/a) -> das ist unabhängig vom a, es wird immer halbiert. Also auch wenn dort
g(x) = 3x² + 9x + 15
stehen würde und du es zu
g(x) = 3[x² + 3x] + 15
umwandelt hättest, würde aus den 3x dann 2 * 1,5 werden. Bei dir wäre das so weit also:
g(x) = 2x² - 10x + 15
= 2[x² - 5x] + 15
= 2[x² - 2*2,5x] + 15
Nun nimmst du die 2,5 und setzt sie als Quadrat einmal positiv und einmal negativ dahinter. Das verändert die Gleichung nicht, denn:
2,5² - 2,5² = 0
Also:
= 2[x² - 2*2,5x + 2,5² - 2,5²] + 15
Nun wird es einfach, du fasst x² - 2*2,5x + 2,5² zusammen basierend der binomischen Formeln:
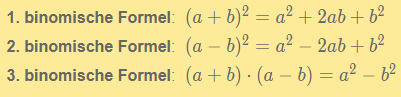
Welche passt von der Form her? Genau, die zweite. Fasst sich also zusammen zu:
x² - 2*2,5x + 2,5² = (x - 2,5)²
Damit wären wir jetzt bei
g(x) = 2[(x - 2,5)² - 2,5²] + 15
Jetzt die -2,5² ausschreiben, damit wir es mit der 15 später verrechnen können:
g(x) = 2[(x - 2,5)² - 6,25] + 15
Wir lösen die eckigen Klammern auf, in dem wir alles mit dem Faktor 2 verrechnen.
g(x) = 2*(x-2,5)² - 2*6,25 + 15
g(x) = 2(x-2,5)² - 12,5 + 15
g(x) = 2(x-2,5)² + 2,5
Ansonsten guck mal noch hier vorbei:
https://studyflix.de/mathematik/normalform-und-scheitelpunktform-4426
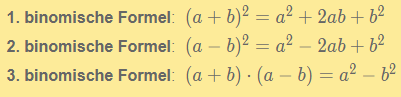
Zunächst wird der in der 2. Zeile vor x stehende Faktor erst halbiert und dann quadriert. Dieser Zahlenwert wird dann in der 3. Zeile erst addiert und dann wieder subtrahiert. Dadurch findet keine Wertänderung statt.
in der 4. Zeile wird dann dieser subtrahierte Teil aus der Klammer herausgenommen
Dadurch wurde die Klammer zu einem reinen Quadrat.