Quadratische Funktionen: Wann pq-Formel, wann quadratische Ergänzung?
Hey, folgende Frage:
In meinem Kurs gibt es zur Lösung quadratischer Gleichungen - unmittelbar hintereinander erläutert - die pq-Formel
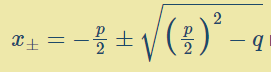
und dann einen anderen Fall, in dem die quadratische Ergänzung verwendet wird, um eine quadratische Gleichung zu lösen
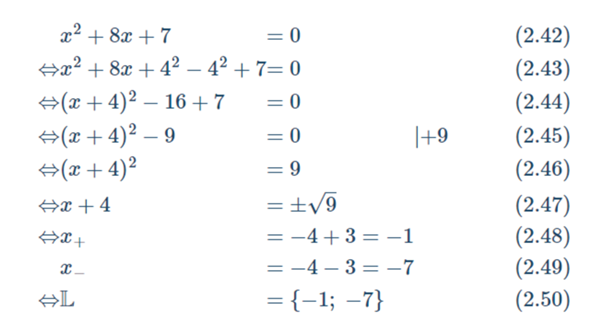
Soweit ich das verstehe, sind es zwei unterschiedliche Methoden, die zum selben Ergebnis führen. Ist das korrekt? In welchen Fällen sollte ich nun vorzugsweise die eine und in welchen Fällen die andere anwenden?
5 Antworten
Die pq-Formel ist das Ergebnis, wenn man die allgemeine quadr. Gleichung x²+px+q=0 mithilfe der quadr. Ergänzung nach x auflöst.
D. h. wenn die pq-Formel bekannt ist, würde ich diese auch direkt verwenden, somit hast Du den kompletten Rechenweg über die quadr. Ergänzung und somit auch Zeit gespart. Ähnlich wie bei den binom. Formeln: wer weiß, dass (a+b)²=a²+2ab+b² ergibt, wird nicht (a+b)*(a+b) einzeln zu a²+ab+ba+b² ausmultiplizieren und dann die ab's noch zusammenfassen.
Als ich nur gelegentlich mal gem. quadr. Gleichungen lösen musste, hab ich das mit quadr. Ergänzung gemacht, da ich mir da die Formel schlecht merken konnte. Jetzt nehme ich eigentlich immer die Formel (die ja nur die allgemeine mit quadr. Ergänzung ist).
Ansonsten
Quadratische Funktionen: Wann pq-Formel, wann quadratische Ergänzung?
Das ist de-facto dasselbe, denn die pq-Formel leitet man mittels quadratischer Ergänzung her (kannst Du mal zur Übung machen). Insofern stellt sich Deine Frage gar nicht, sondern Du benutzt das, was in der Aufgabe gefordert ist und wenn keine bestimmte Methode verlangt wird, das, was Du am besten beherrscht. Da beide Methoden eine Lösung liefern (sofern es eine gibt), sind die Ergebnisse dann auch identisch.
Die pq-Formel lässt sich mittels quadratischer Ergänzung herleiten.
Wenn du die pq-Formel kennst, würde ich sie immer anwenden, es sei denn in einer Aufgabe steht explizit, dass du mit der quadratischen Ergänzung arbeiten sollst.
Soweit ich das verstehe, sind es zwei unterschiedliche Methoden, die zum selben Ergebnis führen. Ist das korrekt?
Ja. 🙂👍
In welchen Fällen sollte ich nun vorzugsweise die eine und in welchen Fällen die andere anwenden?
Das hängt von der persönlichen Vorliebe oder der Aufgabenstellung ab.