Mathe Hilfe?
Hey Leute ich brauche Hilfe zwar beim ausklammern nullstelle berechnen ich hab die erste nullstelle berechnet mit ausklammern aber bei 2te muss ich pq formal anwenden aber am Ende kommt das falsche Ergebnis raus
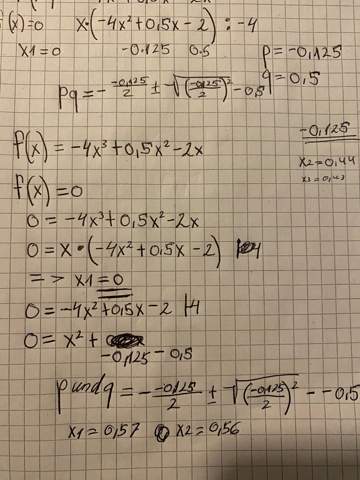
J
3 Antworten
bei 2te muss ich pq formal anwenden
Ja. Die PQ-FORMEL
aber am Ende kommt das falsche Ergebnis raus
Dann wirst Du Dich verrechnet haben. Zeig mal Deine Rechnung.
Bei der PQ-FORMEL kommt kein falsches Ergebnis raus. 🫣😉
Was bedeutet es denn, wenn unter der Wurzel eine negative Zahl steht? 😉
Das weiß ich nicht 🤷♂️ halt in der Wurzel muss ja -0,125 Bruchstich 2 Klammern zu und hoch 2
Ok, dann ein anderer Versuch: Erstell mal eine Wertetabelle im Bereich von x=-1 bis x=+1 in 0,5er Schritten.
Hab ich gemacht also bei x 0 kommt auch null raus aber die nullstelle hatte ich ja mit ausklammern schon berechnet
Das heißt also, dass es keine weiteren Nullstellen gibt. 😁
Wenn Du bei der PQ-FORMEL unter der Wurzel eine positive Zahl hast, gibt es zwei Nullstellen, bei einer Null unter der Wurzel nur eine (doppelte) Nullstelle, und bei einer negativen Zahl keine Nullstellen.
können sie vllt erklären was ich machen muss bei pq formal schreibe übermorgen Arbeit und versteh es nicht 😔
Ich fand das nur komisch das alle sagten berechne weiter mit pq formal obwohl es ja eig nicht ging weil es keine weitere nullstelle gibt
Dass es keine weiteren Nullstellen gibt, muss man ja (z.B. mit Hilfe der PQ-FORMEL) erstmal feststellen.
Also hat es beim den Fall nur eine nullstelle oder 2 doppelte nullstellen wegen null ?
Wegen 0,5 x2 theoretisch könnte man ja x2 klammern anstatt nur x aber man macht mit den kleinsten exponenten deswegen doch nur x ausklammern . Hat sich geklärt viel danken sie haben meine Arbeit gerettetttt 🙏
Du mußt die letzte Gleichung durch -4 dividieren dann ergibt sich
x^2 -1/8 x + 1/2 = 0
Und was ist jetzt deine Frage?
Und was ist das falsche Ergebnis, welches du erhalten hast?
Es wäre nicht schlecht, deine vollständige Rechnung zu sehen.
Falsch geteilt:
.
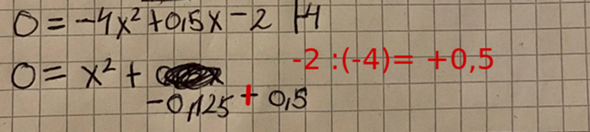
pq-Formel:
x² - 1/8 x + 1/2 = 0
p = -1/8 und q = 1/2
Wenn man nur die Subtraktion unter Wurzel der Wurzel durchführt, erhält man eine negative Zahl, -127/256. Von negativen Zahlen lässt sich schwer eine Wurzel ziehen. Das bedeutet, dass die pq-Formel hier "zu Ende" ist, keine weiteren Nullstellen liefert. f(x) = -4x³ + 0,5x² - 2x hat nur eine Nullstelle bei x = 0.
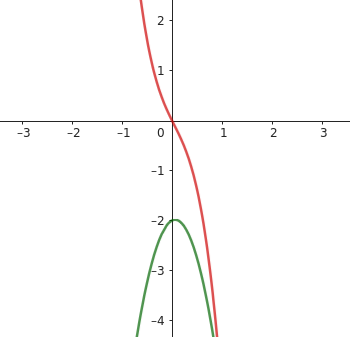
Skizze von
f(x) = -4x³ + 0,5x² - 2x in rot
und
g(x) = -4x² + 0,5x - 2 in grün
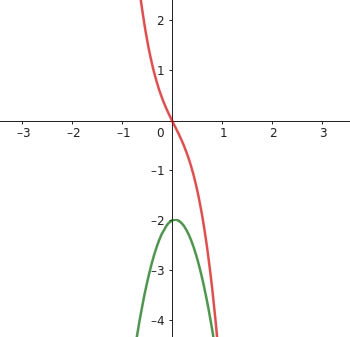
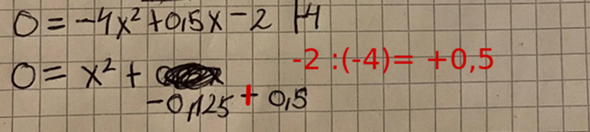
Aber wenn ich dann die Zahlen in pq formal eingebe kommen vollig falsche Ergebnisse raus
Was ist ein völlig falsches Ergebnis in deinen Augen?
Es wäre nicht schlecht, deine vollständige Rechnung zu sehen.
du hast falsch durch -4 geteilt. siehe oben oder die Antwort von Littlethough oder deine eigne Antwort von 18:51.
Aber wenn ich es in Taschenrechner eingebe genauso so nur das halt am Ende nur minus 0,5 ist kommt kein Ergebnis raus was haben sie denn raus bekommen ?
Wenn ich aber p und q formal benutze kommt völlig falsches Ergebnis raus spricht gar keins p ist =-0,125 und q =0,5