Mathe Gleichungen lösen?
Hallo Leute ,
Ich brauche Hilfe ,
könntet ihr mir bitte das genau erklären warum und wie?
(x+5) hoch 2 - 25 = 15
2 Antworten
Erst mal auf "Normalform"
x² + px + q = 0
bringen:
(x + 5)² - 25 = 15 ⇔ | -15
(x + 5)² - 40 = 0 ⇔ | 1.BiFo
x²+10x+25- 40 = 0 ⇔
x² + 10x - 15 = 0
Jetzt gibt es theoretisch vier Lösungsmöglichkeiten:
▪︎ Anwendung der p-q-Formel:
x² + px + q = 0 ⇒
x₁,₂ = -ᵖ/₂ ± √[(ᵖ/₂)²-q]
Hier gibt das
x² + 10x + 15 = 0 ⇒
x₁,₂ = -¹⁰/₂ ± √[(¹⁰/₂)²-15]
= -5 ± √[ 5² - 15 ]
= -5 ± √[ 25 -15 ]
= -5 ± √10
also
x₁ = -5 + √10 ≈ −1,8377223398
x₂ = -5 - √10 ≈ −8,1622776602
▪︎ Faktorisieren nach dem Satz von Vieta. Dazu sucht man zwei Zahlen u und v so, dass u+v = p und u•v = q.
Dann kann man x²+px+q=0 zu (x+u)(x+v)=0 umschreiben, und nach dem Satz vom Nullprodukt ("Ein Produkt ist 0, wenn mindestens einer der Faktoren 0 ist.") schließen, dass (x+u)=0 oder (x+v)=0 sein muss, und somit x₁=-u bzw. x₂=-v.
Das ist hier aber ziemlich sinnlos – ich glaube, niemand findet diese Zahlen ohne die o.g. Formel.
▪︎ Die dritte Möglichkeit wäre die "quadratische Ergänzung" – die kriege ich aber nicht mehr auf die Reihe 🙁. Ich weiß nur noch, dass man daraus die o.g. p-q-Formel herleitet, es käme also aufs Gleiche hinaus 😉.
▪︎ Und die vierte Möglichkeit wäre die Anwendung der sogenannten "Mitternachtsformel" oder "a-b-c-Formel":
ax² + bx + c = 0 mit a≠0 ⇒
x₁,₂ = { -b ± √[(b²-4ac] } / 2a
Aber zum einen haben wir hier sowieso keinen Koeffizienten vor dem x². Zum anderen habe ich nie verstanden, warum man sich diese viel kompliziertere¹ Formel merken soll, wenn man doch einfach die ganze Gleichung durch a teilen und dann die einfachere p-q-Formel anwenden kann. 😉
____________________
¹ OK, wenn man sie so schreibt

sieht sie etwas weniger kompliziert aus, ist aber m.E. immer noch komplizierter als die p-q-Formel

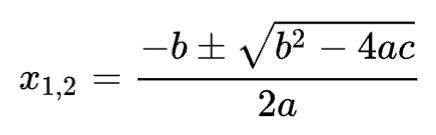

(x+5) hoch 2 - 25 = 15
(x+5) hoch 2 = 40
(x+5) = √40
(x+5) = 6.32455532034
x = 6.32455532034 - 5 / x = 1.32455532034
Kann sein das ich Falsch liege, in Mathe hatte ich fast immer ne 5