Konvergent + Monoton => Alternierend?
Wenn eine Folge konvergent und nicht monoton ist, dann ist sie alternierend.
Ich denke die Aussage ist wahr, aber kann sie nicht beweisen. Ist es tatsächlich wahr denn?
2 Antworten
Vom Beitragsersteller als hilfreich ausgezeichnet
Nein.
Die Aussage ist falsch.
Alternierend bei Folgen bedeutet, daß die Differenz zwischen Wert der Folge und tatsächlichem Grenzwert immer wieder das Vorzeichen wechselt.
Zum Beweis genügt ein Gegenbeispiel:
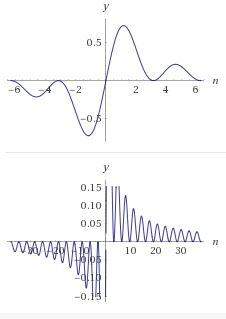
f(n) = sin²(n)/n
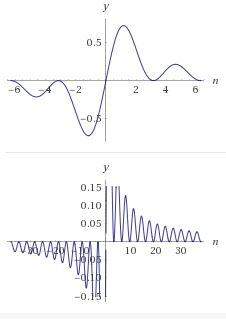
Konvergent und nicht monoton.
trotzdem nicht alternierend.
Die Differenz zum tatsächlichen Grenzwert Null ist immer positiv.
Roderic
02.05.2020, 23:17
@wasistmeinname
Wie gesagt: Zum Widerlegen einer Aussage genügt ein einziges Gegenbeispiel.
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Mathematik
Kannst du vllt die genaue Aufgabenstellung geben?
1+1/n*(-1)^n konvergiert zum Beispiel gegen 1, ist nicht monoton und immer positiv
Vielen Dank! Ich habe ja diese Folge nicht bemerkt