Gemeinsame Punkte einer Funktionsschar bestimmen,?

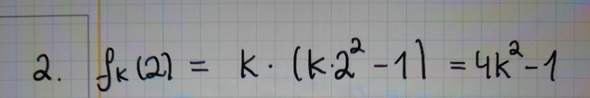
Hallo ich blicke hier nicht ganz durch. Ich soll die Funktionenschar auf gemeinsame Punkte untersuchen. Als erstes habe ich für k zwei unterschiedliche Werte eingesetzt, beide Funktionen gleichgesetzt und nach x aufgelöst. Jetzt muss ich aber noch den y Wert berechnen indem ich den x Wert in die Funktion einsetze. Aber da kommt 4k^2-1 raus. Ist das falsch? Kann mir bitte jemand helfen

Answer 1

[evtldocha]

Deine Idee ist schon richtig - allerdings darfst Du nicht bestimmte Werte für k einsetzen, sondern Du musst ein k₁ und ein k₂ verwenden. Dann ergibt das eine Gleichung und daraus ergibt sich eine Nullstellensuche. Wenn eine (oder alle) gefundene Nullstellen dann unabhängig von k₁ und k₂ sind, dann hat die Funktionenschar einen (oder mehrere) gemeinsamen Punkt(e).

Hier:

$k_1\cdot\left(k_1x^2-1\right)\ =\ k_2\cdot\left(k_2x^2-1\right)$

$→(k_1^2​−k_2^2​)\cdot x^2=k_1​−k_2$

$\rightarrow\ x^2=\frac{k_1-k_2}{\left(k_1+k_2\right)\cdot\left(k_1-k_2\right)}$

$\rightarrow\ x_{1/2}=\pm\ \frac{1}{\sqrt{k_1+k_2}}$

Der Schnittpunkt der Funktionen hängt also von der Wahl von k₁ und ein k₂ ab und daher hat die Funktionenschar keinen gemeinsamen Punkt.

Answer 2

[Halbrecht]

k1 = a , k2 = b ( wegen Lesbarkeit)
.

:

a*(ax²-1) = b*(bx²-1)

a²x² - a = b²x² - b

x²*(a²-b²) - (a-b) = 0 

durch (a² - b)²

x² - 1/(a+b) = 0 

x² = +1/(a+b) 

x = +- wurzel(1/(a+b))

.

Beispiel für a = 4 und b = 5 

wurz(1/9) = + - 1/3

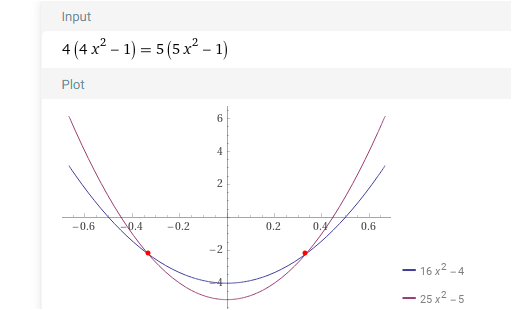
und nun : was noch machen damit ? wird basteln uns einen Schnittpunkt bei x = 0
jerk ; geht gar nicht :((..............weil 1/(a+b) nicht Null werden kann , darf )

Was wenn a = -b ? ......................Kein Schnittpunkt

ich will , dass bei +1 und -1 schnittpunkt ist

w(1/(a+b)) ................a+b muss +1 werden ...............das ist bei a=4 und b=-3 oder vielen anderen Paaren der Fall

Lustigerweise hast du genau das gezeigt : denn k = 0 + k = 1 ist 1 , also schnittpunkt bei x = 1 ,,,,,,,,,,,,weil aber fk1(1) = 0 und fk2(1) = 0 könnte man denken , dass es ein gemeinsamer Punkt ist.

aber mit k = 0 hast du aus einer Parabel die Fkt f_k=0_(x) = 0 gemacht , also die x Achse

Answer 3

[Letzi]

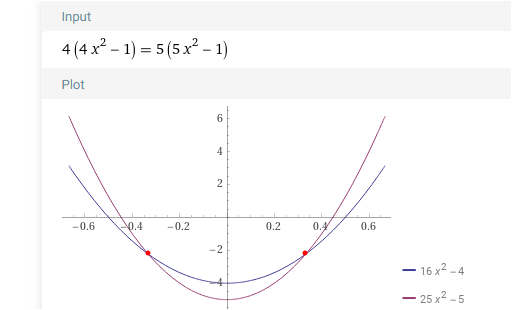
Du hast auf dem oberen Bild nur die Schnittpunkte für 1 und 0 und nicht für alle k bestimmt