Funktion f(x)=ax^2 bestimmen sie a so, dass…?

Hallo zusammen,

kann mir wer bei der Folgenden Aufgabe helfen, komme irgendwie nicht voran…

Gegeben ist die Funktion f mit f(x)=ax^2. Bestimmen sie a so, dass

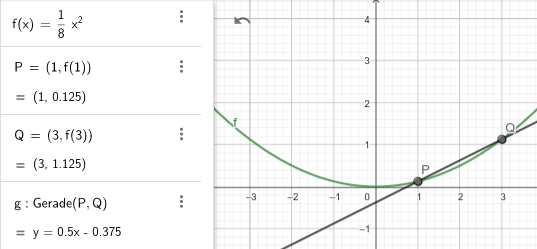
a) die durchschnittliche Änderungsrate im Intervall [1;3] den Wert 1/2 annimmt;

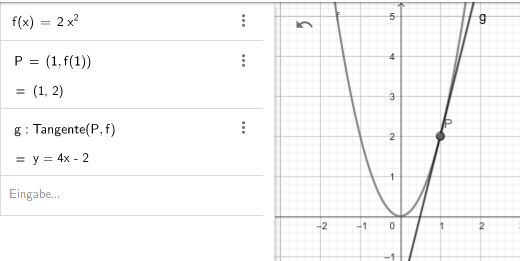
b) die Tangente an den Graphen von f im Punkt P[1/f(1)] die Steigung 4 besitzt;

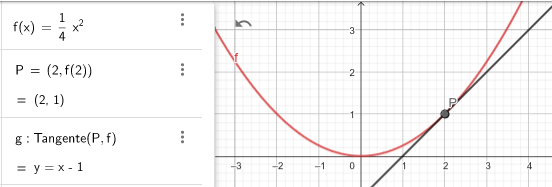
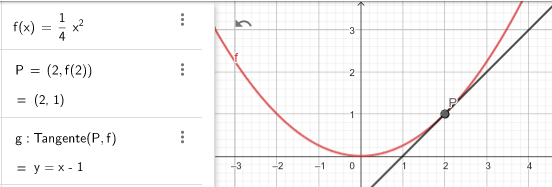
c) die Tangente an den Graphen in Q[2/f(1)] die x-Achse unter einem Winkel von 45 grad schneidet.

Danke schon mal im Voraus

LG ☺️

Answer 1

[evtldocha]

Aufgabe a) übersetzt sich in:

$\frac{f\left(3\right)-f\left(1\right)}{3-1}=\frac{9a-1a}{2}=\frac{1}{2}\rightarrow\ a\ =\ \frac{1}{8}$

Skizze:

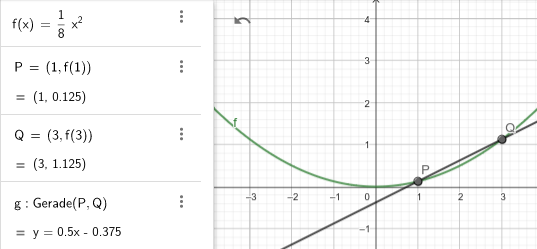
Aufgabe b) führt zur Gleichung

$f'\left(1\right)=2a\cdot1=4\ \rightarrow\ a\ =2$ Damit $f\left(x\right)=2x^2$

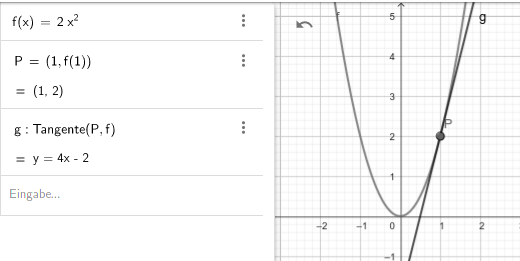
Aufgabe c) führt zur Gleichung (kleiner Typo in Deiner Frage: Der Tangenten-Punkt muss natürlich Q[2 | f(2)] sein und nicht Q[2/f(1)])

$f'\left(2\right)=\tan\left(45°\right)=1$

Also:

$f'\left(2\right)=2a\cdot2=1\rightarrow\ a=\frac{1}{4}$