Bestimmtes Integral berechnen (Partielle Integration)?
Hallo zusammen,
ich bin mir nicht sicher, wie ich bei diesem Integral vorgehen soll.
Mein erster Gedanke war partielle Integration. Aber wie kann man von ln(sinx) die Stammfunktion bilden? Oder gibt es einen einfacheren Weg?
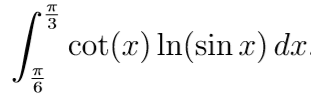
4 Antworten
... hat es in sich, finde ich.
Letzer Ausweg
Also tatsächlich geht es mit partieller Integration, der offensichtliche Weg wäre wie die anderen gesagt haben Substitution, aber partielles Integrieren ist der gleiche Weg auf eine andere Art.
Ich hab mal beide Wege aufgeschrieben. Für das partielle Integrieren nutze ich die DI-Methode damit ich mir die „Formel“ merken kann aber ist auch nichts anderes als u und v zu bilden und dann die Formel anzuwenden.


keine partielle integration, substitution ist hier gefragt, die erste funktion ist nämlich die ableitung der zweiten, den rest solltest du erst mal selbst herausfinden
Heißt das ich muss Substitution und partielle Integration gleichzeitig in dieser Aufgabe anwenden?
Hmmm... also ich verstehe jetzt nicht wie cotx die Ableitung von sinx ist?
Soweit ich weiß guckt man sich den Wert in der Funktion an... also hier was im Logarithmus steht :/
Ich schreibe jetzt mal eine eigene Antwort:
Substituiere u=ln(sin(x)) und leite u nach x ab, dann dürfte das weitere Vorgehen klar sein.
also ich verstehe es irgendwie immer noch nicht.
Wenn ich ln(sinx) ableite dann bekomme ich cosx/sinx was auch der cotx ist.
Ich weiß aber nicht wie ich weiter vorgehen soll. Im Skript steht:
f(g(t))g'(t) dt und man soll nur das g(t) substituieren. Das verwirrt mich jetzt.
Definiere dir f(t)=t und gehe dann vor wie im Skript. Dann sollte es klappen.
Nein cot(x) ist nicht die Ableitung von sin(x). Die Substitution von ln(sin(x)) ist zielführender.