Wie wende ich die Partielle Integration auf folgende Aufgabe an?
Ich habe das folgende Integral:
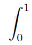
Und ich weiß nicht, wie genau ich da nun partiell Integrieren soll...
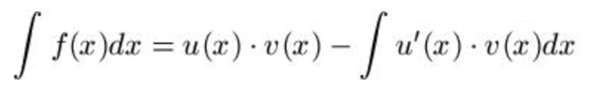
Von e^(x^2) kenne ich die Stammfunktion nicht, weshalb ich die Stammfunktion von 2x^2 bestimmt habe, jedoch kennt man am Ende nicht die Stammfunktion vom Integral des Ergebnisses nicht. Also bringt mir mehrfache partielle Integration nichts, richtig?
4 Antworten
Das ist noch Schulstoff ?
beim Integrieren taucht erfi auf

Am Anfang nutzt man noch die pInt aber dann muss man was wissen ( und auch daraufzusteuern)



Ich würde dir empfehlen es zusätzlich mit der Substitution u=x^2 zu versuchen.
Es übersteigt den Rahmen eine Stammfunktion der Exponentialfunktion anzugeben. Da du ein Integral mit endlichen Grenzen hast, sollte es ja kein Problem sein die Substitution anzuwenden.
Die Stammfunktion der Funktion wie sie da steht ist eindeutig bis auf eine Integrationskonstante und da kommt man nicht drum herum.
Aber mit einer Substitution änderst du ja die Funktion grundsätzlich, damit kannst du einen anderen Rechenweg einschlagen.
Na, an diesem Integral wirst Du Dir die Zähne ausbeißen:
https://www.wolframalpha.com/input/?i=f%28x%29%3D2x%5E2+*+e%5E%28x%5E2%29
Die Stammfunktion von e^(x²) enthält nämlich die komplexe Fehlerfunktion erfi(x).
Hallo Kek238238,
Tipp: Substituiere zuerst x^2 durch z
damit
Der Rest ist Dir sicher geläufig
MFG automathias
integralrechner.de sagt ja : erf i ist im spiel . meinst du , man kann dies mit einer Substitution umgehen ?