Wurden heir zu viele Integrale gebildet? (0.9-Quantil bestimmen, mit Verteilungsfunktion)?
Es geht um die Aufgabe 65:

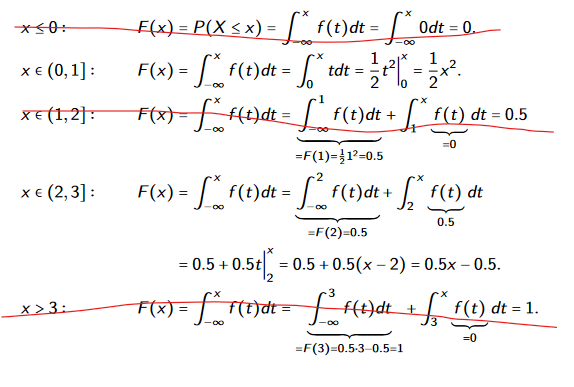
Hier bei dem Beispiel wurden alle möglichen Intervalle berechnet, aber wirklich nötig, wären doch immer nur die, wo auch die FUnktion defineirt ist, also [0,1] und [2,3], klar ist es im Bereich von [1,2] auch irgendwo definiert gewesen, weshalb ein Wert rauskommt, aber kann man im allgemeinen Sagen, dass man nur immer, ebi solchen Aufgaben, wo ich die jeweilige Verteilungsfunktion suche, die Integrale bestimmt, wo das x genau in einem Intervall liegt, welches auch ind er FUnktion klar angegeben ist? Wie [0,1] und [2,3]?
1 Antwort
Die Dichtefunktion ist auf ganz ℝ definiert. Diese wird dabei mit Indikatorfunktionen ausgedrückt:Mit solchen kann man abschnittsweise definierte Funktionen ausdrücken, also:
Die Funktion ist in dem sonst-Fall nicht undefiniert sondern 0.
Für die Verteilungsfunktion an der Stelle x integriert man von -∞ bis x. Das Integral berechnet man, indem man abschnittsweise die Stammfunktionen bestimmt und die Integrale aufsummiert.
Bei Indikatorfunktionen sind die außerhalb der Mengen liegenden Abschnitte durch 0 definiert.
Die Integrale über diese Abschnitte müssen definitionsgemäß auch bestimmt werden, nur sieht man es hier schnell, dass da 0 rauskommt.
Der Rechenweg ist nachvollziehbarer, wenn man explizit hinschreibt, dass da 0 rauskommt.
z.B. der Median, also das 50%-Quantil, liegt dort (ist nicht immer eindeutig), wo F(x)=0,5 ist. Und das ist im ganzen Intervall [1,2] der Fall, z.B. kannst Du 1,28972 als Median nehmen, oder auch 1,5 als Mitte aller möglichen in Frage kommenden Werte, wie man es häufig macht. Damit liegt das 50%-Quantil in einem Abschnitt der Verteilungsfunktion, der konstant ist.
So einen Abschnitt bezeichnest Du wohl als einen, in dem die Funktion nicht klar angegeben ist. Aber sie ist überall klar angegeben. OK, die Dichte ist hier 0, aber die Verteilungsfunktion summiert ja die Fläche zwischen der x.Achse und der Dichtefunktion zwischen -unendlich und dem jeweiligen x
Danke, aber es reicht doch allgemein immer, dass man nur die die direkt genannten Abshcnitte überprüft? Also Integral , wo x Element von 0 bis 1 und das Integral wo x Element von 0.5 ist, bestimmt? Ich hätte jetzt nicht noch die anderen Integrale, wie in der Lösung oben bestimmen müssen? Ich kann davon ausgehen, dass das QUantil immer in einer der Verteilungsfunktionen ist, wo ich direkt die Integralgrenzen nehme, die auch ind er FUnktion klar angegeben sind? Also Integral von 1 bis 2 müsste ich eigentlich nicht beachten, da die chance, dass es da vorkommt nicht möglich ist?