Woher weiß ich, ob diese Dreiecke ähnlich sind?
Warum sind diese drei Dreiecke ähnlich? Also, welche Winkelsätze sind hierbei vorhanden?
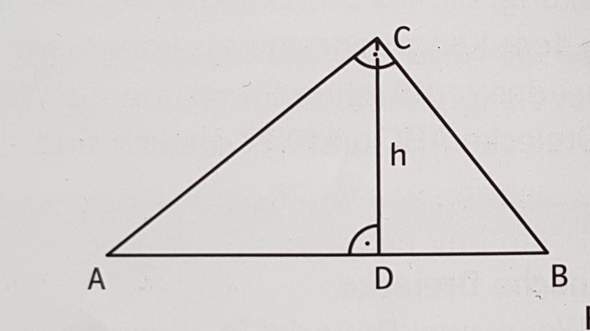
Vielen Dank
4 Antworten
Dreieck 1 = ABC
Dreieck 2 = ADC
Dreieck 3 = DBC
Dreieck 1 hat einen rechten Winkel bei D. Dreieck 2 und 3 haben einen rechten Winkel bei D.
Dreieck 1 => 180° = 90° (C) + Winkel A + Winkel B
Dreieck 2 => 180° = 90° (D) + Winkel A + Winkel C2
Dreieck 3 => 180° = 90° (D) + Winkel B + Winkel C3
Also
Dreieck 1 = Dreieck 2 weil Winkel B = Winkel C2
Dreieck 1 = Dreieck 3 weil Winkel A = Winkel C3
Die Frage lautete: Also, welche Winkelsätze sind hierbei vorhanden?
Trotzdem helfen den FS deine Gleichungen nicht weiter.
Ich glaube, hier gibt es, wie immer in der Mathematik, ein Problem mit dem Wort „ähnlich“;
Denn nur weil sich etwas ähnlich verhält, ist es ja nicht direkt gleich. Und darauf will man hier raus.
du unterteilst das rechtwinklige Dreieck ja in zwei kleinere. Beide (daraus entstehende Dreiecke) haben auch wieder, wie der „große Papa“ einen rechten Winkel, dazu noch zwei Katheten (kurze Dreieckseiten) und eine Hypotenuse (längste, dem rechten Winkel gegenüber liegende Seite).
Sowohl das große Dreieck, wie auch die kleinen Dreiecke besitzen den Winkel α, β, γ. Dies ist aber in deiner Zeichnung nicht zu erkennen, da die Winkel nicht eingezeichnet sind.
nichtsdestotrotz hat jedes Dreieck mit einem rechten Winkel im Inneren immer 180 Grad in seiner Summe.
Daher ist nicht jedes Dreieck gleich, sie verhalten sich nur gleich.
Alle Dreiecke bieten dir also die selben Möglichkeiten zur Berechnung der Seiten und des Flächeninhalts, die Seiten und der Flächeninhalt jedoch selber ändern sich immer (weil ja auch logischerweise die Dreiecke irgendwo entzweit werden).
Warum holst du so weit aus? Zwei Dreiecke sind ähnlich, wenn sie in zwei Winkeln gleich sind (damit stimmen sie auch im dritten Winkel überein). Hier haben die kleinen Dreiecke einen rechten und einen weiteren gemeinsamen Winkel mit dem großen Dreieck.
Ich hole soweit aus, weil der FS scheinbar die Basis des ganzen nicht verstanden hat.
Hast du ein Problem damit? Falls ja, befasse dich bitte selbst damit. Denn falsch ist meine Antwort gar nicht.
Kurz zusammengefasst: die drei Dreiecke verhalten sich ähnlich, sind aber nicht gleich.
Von Gleichheit ist in der Frage aber auch keine Rede. Der FS fragt gezielt nach Winkelsätzen. Sollte die Frage anders gelautet haben, als du sie beantwortet hast, will ich nichts gesagt haben.
Du redest und redest ... aber Du hast entweder die Frage verstanden oder keine Ahnung von Geometrie.
nichtsdestotrotz hat jedes Dreieck mit einem rechten Winkel im Inneren immer 180 Grad in seiner Summe.
Falsch.
Jedes Dreieck hat eine Winkelsumme von 180°. Nicht nur solche, die einen rechten Winkel haben.
Ich glaube, hier gibt es, wie immer in der Mathematik, ein Problem mit dem Wort „ähnlich“;
Das ist kein Problem. Ähnlichkeit hat in der Geometrie eine feste Bedeutung.
Die können nicht gleich sein, da es NUR einen rechten Winkel (D) gibt.
Die Winkel bei C sind unterschiedlich und KEINE 90 ° denn sonst hätte da ein Punkt drinne sein müssen
Es geht nicht um gleich, sondern um ähnlich.
Die Dreiecke stimmen in allen drei Winkeln überein, sowohl die beiden Teildreiecke als auch das große Dreieck.
Setze bitte mal eine Brille auf. Wenn zwei Dreiecke in allen Winkeln gleich sind, müssen sie auch, logischer Weise, gleich groß sein. Sind sie aber hier nicht!
Wenn zwei Dreiecke in allen Winkeln gleich sind, müssen sie auch, logischer Weise, gleich groß sein.
Falsch, total falsch.
das sind aber dann auch BEIDE Winkel die zusammen 90 ° ergeben
Dieser Winkel wird aber doch durch die Höhe h geteilt! 🤣😂🤣😂
Na, da haben wir aber zwei Schlauberger!
Ach ja, Schlauberger. Die Dreiecke sind aber trotzdem zueinander ähnlich.
Da das grosse und die beiden kleinen Dreiecke schon mal den rechten Winkel gemeinsam haben muss noch ein Winkel gemeinsam sein um die Ähnlichkeit herzustellen.
Hier nachzulesen: https://www.arndt-bruenner.de/mathe/geometrie/euklid1.pdf&ved=2ahUKEwj40smm36XmAhVt5aYKHRN5CZIQFjADegQIARAB&usg=AOvVaw1UKlelATjNWE5wCasG85oS&cshid=1575799217933
If you're gonna mock me get your facts straight ;)
Ich fürchte, Dir fehlen da grundlegende geometrische Kenntnisse.
Hallo,
sie stimmen in allen drei Winkeln überein.
Herzliche Grüße,
Willy
Also sie stimmen ja im rechten Winkel überein, aber was ist mit dem Rest? Ein Winkel reicht ja nicht um von Ähnlichkeit zu sprechen.
In den anderen auch, weil das große Dreieck ebenfalls rechtwinklig ist.
Den Winkel bei B haben das große Dreieck und das rechte Teildreieck gemeinsam, ebenfalls den rechten Winkel. Dann muß wegen des Innenwinkelsummensatzes der dritte Winkel bei den beiden Dreiecken auch gleich sein.
Das gleiche gilt für das linke Teildreieck (gemeinsamer Winkel bei A und rechter Winkel) und das große Dreieck.
Ok, das heißt also ABC und ADC sind ähnlich und ABC und BCD sind ähnlich.
Aber warum sind dann ADC und BCD ähnlich?
Das stimmt nicht! Winkel A, B und C sind in beiden Dreiecken nicht gleich, nur der Winkel an Punkt D ist bei beiden Dreiecken ein Rechter Winkel, also 90Grad.
Dann hast Du nicht richtig hingesehen. Der Winkel bei C im großen Dreieck ist ebenfalls ein rechter Winkel (er ist mit einem Punkt gekennzeichnet).
Und deine stumpfen Gleichungen sollen einem Fragesteller, der scheinbar die Basis des Ganzen nicht verstanden hat, sinnvoller sein, als mein etwas längerer, aber zumindest in Textform verfasster Ansatz?
Wenn das was du hier aufschreibst jemandem hilft, der Schwierigkeiten mit dem Verständnis hat, bringen ihm/ihr deine Gleichungen, die du leblos dahinklatscht keine Hilfe.
Und bedenke bitte eines; lernen kann jeder, lehren jedoch nicht. Zu letzterem gehörst eindeutig du!