Fehlende Seitenlängen von Dreiecken berechnen?
Kann wer sagen, wie ich das rechnen muss? Den Satz des Pythagoras hatten wir bislang noch nicht durchgenommen.
(Die Dreiecke sind ähnlich)
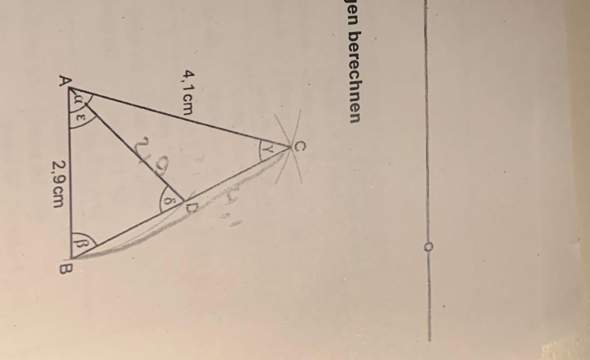
Es ist gleichschenklig
3 Antworten
Berechnung ist nach folgenden PDF möglich. Die roten Maße sind ja gegeben.
http://texxtorr.bplaced.net/gf/Berechnungen/Dreieck/gf-20211221-2303-001.pdf
Würde sagen das ist nur machebar wenn entweder mindestens auch noch ein Winkel bekannt ist oder es ein gleichschenkeliges Dreieck wäre.
[geändert]
Es ist ähnlich. Das sagt das Buch, mein Lehrer und ich.
Und wie gesagt, den Satz des pythagoras will ich dort garnicht anwenden, da ich das noch nicht gemacht habe.
Du hast mich überzeugt. Zwei Seitenlängen sind 4,1 cm lang und zwei Seitenlängen sind 2,9 cm lang. Damit sind die Dreiecke ähnlich. Hieraus kann man den Faktor k errechnen, weil die Seiten ähnlich sind.
k = 4,1 / 2,9 = 1,41
Das heißt BD und AB sind die gleichen Seiten, nur eben um den Faktor k vergrößert.
BD * k = 2,9
Jetzt kannst du nach k auflösen und dann einsetzen
BD = 2,9 / k
BD = 2,9 / 1,41 = 2,05
Es ist gleichschenklig (muss ich noch in der Beschreibung ergänzen, entschuldige)