Wie wäre die Umfang-Formel dieser Figur?
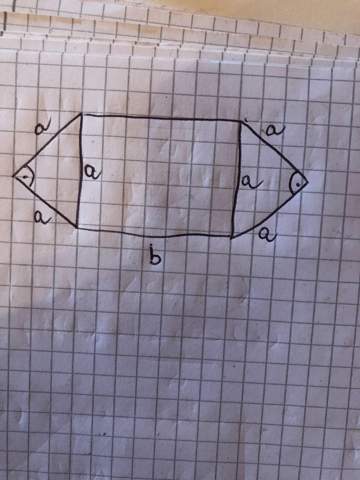
Es soll ein Rechteck mit zwei rechtwinkligen Dreiecken an den Seiten darstellen. Nun, ich bin der Meinung, dass die Formel : U=2b+6a lautet, doch im Internet finde ich nur die Formel U=2b+4a. Wenn diese richtig sein soll, wie kann man sich das erklären, denn wir haben 6mal die Seite a
8 Antworten
Rechteck berechnen und die 2 Dreiecke geben gemeinsam ein Quadrat. Also Quadrat berechnen. Addieren.
Ja, das ergibt Sinn, aber ich werde beispielsweise in einer Klausur nicht erkennen können, dass die zwei Rechtecken ein Viereck bilden
Nun, ich bin der Meinung, dass die Formel : U=2b+6a lautet, doch im Internet finde ich nur die Formel U=2b+4a. Wenn diese richtig sein soll, wie kann man sich das erklären, denn wir haben 6mal die Seite a
- Nehme Dir einen Buntstift (z.B. rot)
- Fahre nur den äußeren Umriss der Figur mit dem Buntstift ab (denn das ist der "Umfang").
Welche Kanten sind jetzt alle rot angemalt? Wie viele Seiten mit einem "b" und wie viele mit einem "a"?
Ich zähle da zweimal "b" plus viermal "a".
Deine Figur bzw. Frage enthält aber zusätzlich ohnehin einen Denkfehler:
Es soll ein Rechteck mit zwei rechtwinkligen Dreiecken an den Seiten darstellen.
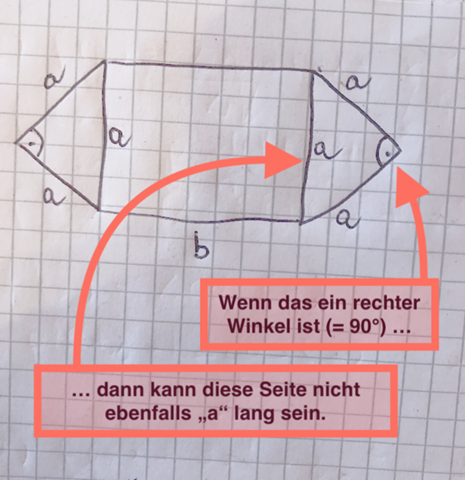
Wenn es rechtwinklige(!) Dreiecke sind, dann kann die Hypotenuse (also die Seite gegenüber dem rechten Winkel) nicht genauso lang sein wie die beiden Katheten (= die Seiten am rechten Winkel).
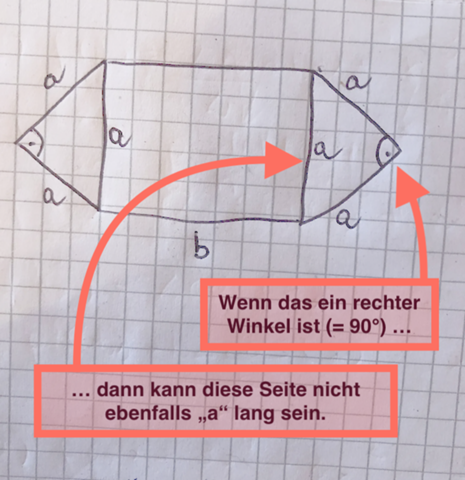
Wenn bei den Dreiecken alle Seiten gleich lang wären, dann wären es gleichseitige Dreiecke (nicht rechtwinklige) und dann sind alle Winkel im Dreieck immer gleich groß und betragen jeweils 60°.
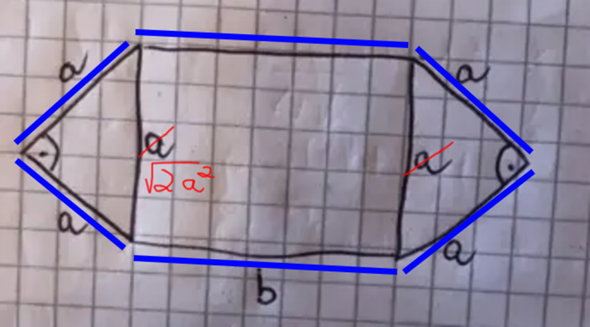
Der Umfang ist die blaue Linie. Das sind 4a + 2b = U
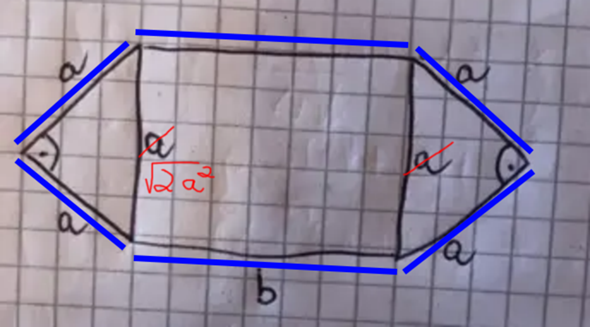
Gemäß dem Satz des Phytagoras ist die Höhe des Rechtecks Wurzel(2a²).
Viel Spaß bei deiner Extremwertaufgabe!
Ist Wurzel(2a^2) nicht die Hypotenuse gemäß Satz des Phytagoras? Als Höhe habe ich auch mit dem Satz des Phytagoras a/Wurzel(2)
Ja und Ja.
Aber die Höhe brauchst du nicht. Die hast du sicher nur zu Übung berechnet ;)
Sollst du den Flächeninhalt maximieren ist die Formel für den Flächeninhalt ein Rechteck mit b * a * Wurzel(2) Plus ein Quadrat a²
max. A = a² + b * a * Wurzel(2)
Umfang U = 4a + 2b
Ich muss den Umfang maximieren, und habe die Information, dass der Flächeninhalt dieser Figur 100 cm beträgt, ich brauche also die Höhe um dann b zu bestimmen
Naja... vielleicht geht ja auch dein Weg. Ich löse das nur mit a und b.
Sollst du wirklich den Umfang maximieren???
Wenn a = 0,1 dann wäre b mit A = a² + b * a * Wurzel(2) = 100
b= 707 und U = 4a + 2b = 1414 m
Bei a = 0,01 wäre b = 7071 und U = 14142 bei A = 100 m²
Also U wird maximal wenn a gegen 0 geht.
Die Aufgabenstellung U zu maximieren kann nicht richtig sein.
Genau! Ich habe schon mal so eine Aufgabe vorgerechnet hier.
denn wir haben 6mal die Seite a
Da ist schon der Denkfehler. Du hast nur 4 mal a. Die 2 a längen am Rechteck sind √2*a, da du einen rechten Winkel hast.
Richtig wäre 4*a+2*b, aber deine Skizze ist falsch.
Umfang Rechteck= 2a+2b
Umfang Dreiecke= (a+b+c)*2
Und dann addieren.
Alle Seiten des Dreiecks sind gleich, ich brauche , dass die Variablen so wenig wie möglich sind…
Aso, dann zählen die inneren a Seiten des Quadrats nicht mit. Also stimmt U=2b+4a!
vielen Dank für die Antwort! Ich habe es jetzt verstanden!