Wie verändert sich die Parabel wenn der Exponent steigt?
Also
x^1, x^3, x^7 —> inwiefern verändert sich die Parabel
und
x^2,x^4,x^6 —> inwiefern verändert sich die Parabel
und
x^-1,x^-3, x^-7—> inwiefern verändert sich die Hyperbel
und
x^-2, x^-4,x^-6—> inwiefern verändert sich die Hyperbel
1 Antwort
Hallo,
für x ∈ ]0, 1[ wird mit steigendem Exponent die Kurve zur x-Achse hin
gedrückt oder gestaucht.
Für x > 1 wird mit steigendem Exponenten die Kurve nach oben
(= in Richtung der y-Achse gestreckt).
Zur Veranschaulichung zwei Bilder:
0 < x < 1 :
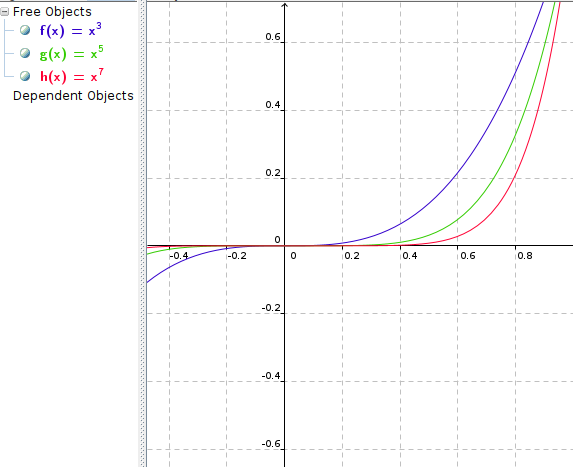
x > 1 :
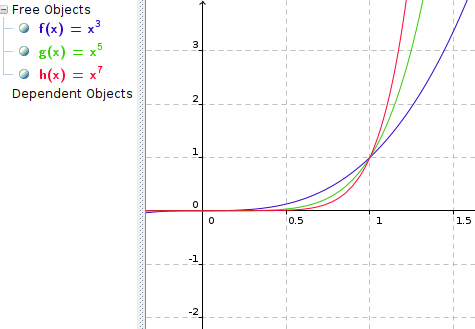
was man auch rechnerisch sieht:
0 < x < 1 | • x =>
0 < x² < x | • x =>
0 < x³ < x²
d.h. aus 0 < x < 1 folgt 0 < x³ < x < 1
Ähnlich kann man für -1 < x < 0 und x < -1 argumentieren, was ich dir überlasse.
Gruß
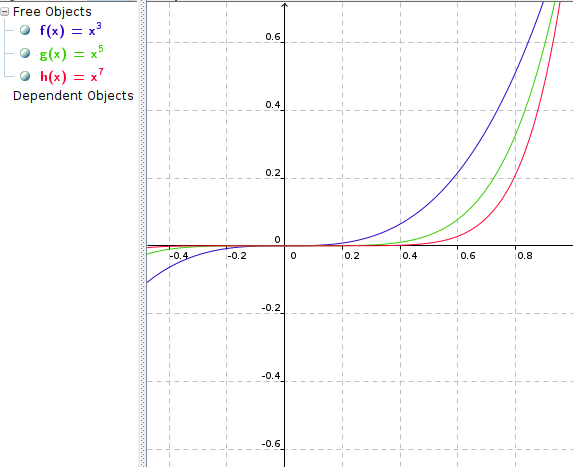
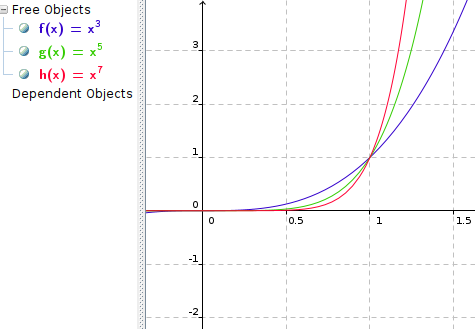
P.S. Genauso :
1 < x | • x
x < x² | •x
x² < x³
d.h. insgesamt: aus x > 1 folgt x³ > x , und x⁵ > x³ > x usw.