Wie Krümmung von geschlossener Strecke bei gegebenen Punkten berechnen?
Hallo, also ich habe folgendes Problem: Gegeben ist in Matlab die Mittellinie einer geschlossenen Rennstrecke in Form einer Matrix mit erster Spalte X-Koordinaten und 2. Spalte Y-Koordinaten....
Nun soll ich für jedes Punktepaar die Krümmung berechnen um Geraden auf der Strecke zu filtern, dabei ist die Krümmung in Abhängigkeit des auf der Strecke zurückgelegten Wegs s definiert (siehe Foto)
etzt habe ich das Problem, dass die X und Y-Koordinaten jeweils eine Funktion in Abhängigkeit von s sein müssen und dann abgeleitet werden.. wie mache ich das? Also ich habe mittlerweile jedem Punktepaar eine Länge s zuordnen können (Approximation über Satz des Phythagoras, weil die Punkte sehr eng beieinander liegen)
Für die erste Ableitung würde ich statt dX/ds einfach z.B (X2-X1/s2-s1) nehmen, wäre das in Ordung? Aber wie soll ich denn die 2. Ableitung mit den Punkten hinbekommen? Könnte ich vielleicht doch irgendwie eine allgemeine Funktion der Koordinaten von s berechnen?
Für Xi würde ja z.B. gelten: Xi(si)= sqrt(((s(i)-(s(i-1))^2-(y(i)-y(i-1))^2) + x(i-1)... aber das wäre doch Quatsch, das nach si abzuleiten, oder?
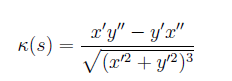
3 Antworten

Mit MatLab ist es sicher kein Problem, aus den Punkten eine glatte Kurve zu berechnen. Allerdings werden dabei (fast) gerade Teilstrecken durch Schwingungen verfälscht, was für Deine Aufgabe eher schlecht ist. Du kannst aus dieser Kurve bestenfalls genauere Werte für ∆s ermitteln. Das ist allerdings ziemlich aufwendig.
Dein Ansatz für ∆s und X'=∆X/∆s ist also völlig ok. Damit berechnest Du die mittlere Steigung zwischen X und seinem Vorgänger (oder Nachfolger).
Die zweite Ableitung geht genauso:
X" = ∆X'/∆s
X" wird hier effektiv aus X und den zwei Werten davor (oder danach) berechnet. Das ist etwas "einseitig". Solange die Punkte wirklich dicht beieinander liegen, sollten sich benachbarte Werte für X' und X" kaum unterscheiden, sodass das nichts ausmacht. Aber es schadet nicht, den Index bei X" um eins zu verschieben (also X"ₙ effektiv aus Xₙ₋₁, Xₙ und Xₙ₊₁ zu berechnen).
Noch genauer wird die Rechnung, wenn Du für X' den Mittelwert aus der Steigung ∆X/∆s davor und danach nimmst. Das ist recht anschaulich, wenn Du den Graphen von X(s) betrachtest: Der Polygonzug hat eine konstante Steigung ∆X/∆s vor X(s), und eine danach. Jede Steigung zwischen diesen beiden wird die wahre Steigung besser annähern als eine der beiden allein.
Jetzt sind X' und ∆X/∆s zwei Paar Stiefel, und Du kannst X" entweder wie oben beschrieben aus ∆X/∆s davor und danach berechnen, oder aus den gemittelten X' und dann wieder den Wert davor und danach mitteln. Dann gehen sogar je zwei Punkte vor und nach X in die Berechnung von X" ein.
Ich persönlich würde das bisschen Mehraufwand nicht scheuen und mit den Mittelwerten rechnen: Wenn die Werte von X und Y größere Sprünge machen, ist das bestimmt genauer. Und wenn sie sich nur in den letzten Ziffern unterscheiden, schlagen die Rundungsfehler vermutlich weniger durch, wenn man mit fünf statt drei benachbarten Punkten rechnet.


ja, tatsächlich. s hat zwischen den Punkten meistens eine Differenz von etwa 0.01, nur an manchen Übergängen folgen 2 gleiche Werte (dann ganzzahlig)

Moment mal: ∆s=√(∆X²+∆Y²) sollte eigentlich nur bei identischen benachbarten Punkten Null werden. Doppelte Punkte (X,Y) würde ich bei Rennstrecken einfach löschen.
Oder berechnest Du erst s=Σ(∆s) und bildest davon wieder die Differenzen? Das wird ungenauer, und wenn MatLab beim Summieren irgendwie 'intelligent' rundet, könnten dabei auch Null-Differenzen entstehen.
Nimm einfach die berechneten Hypotenusen ∆s. Die Summen s werden höchstens zur Ausgabe gebraucht.

Schau mal hier; ich hatte sie nachentdeckt in unserem Elektronikkonzern
https://de.wikipedia.org/wiki/Kubisch_Hermitescher_Spline
Die Hermiteschen Splines; das sind weiter nix als 2 X 2 Unbekannte. Aber wie das so geht - mein Chef glaubte mir erst, als ich ihm nachwies, dass " meine " Kurven in seinem schlauen Buch vorkommen. Also ich kenn das eher mit den vier Basispolynomen; aber musste mal sehen.
Ja und dann erwähnt er noch die ===> Bezierkurven. Überhaupt; besorg dir mal beom ===> Hugendubel gescheite Literatur über die Teorie von Interpolationspolynomen. Die sind nämlich genau für deinen Zweck da.

Ich bin keine Studentin, war es auch nie, deshalb ist die Nützlichkeit meiner Antworten eingeschränkt.
Ich betreibe Mathematik nur als kleines Hobby in der Freizeit; das ist alles.
Besorge dir mal folgendes Buch (das sollte in den meisten Leihbüchereien zu finden sein, musst du also nicht unbedingt kaufen, weil das Buch in seinem Themengebiet "bekannt ist wie ein bunter Hund", und deshalb in den meisten Leihbüchereien in größeren Städten zu finden sein sollte.) :
Hans Rudolf Schwarz, "Numerische Mathematik", B.G. Teubner Verlag
Ich besitze davon die 3-te Auflage.
Kapitel 3 von dem Buch behandelt das Themengebiet "Interpolation"
Kapitel 3.7 behandelt das Themengebiet "Splineinterpolation"
Abschnitt 3.7.5 lautet "Glatte zweidimensionale Kurvendarstellung" und diesem Abschnitt geht das Thema "Splineinterpolation" vorweg, und darauf bezieht es sich auch.
Dort werden die Koordinaten x(t) und y(t) als Funktionen eines Parameters t angesehen. Den Parameter kann man natürlich nennen wie man will.
Zitat aus dem Buch :
Als Kurvenparameter t wäre die Bogenlänge der Kurve am geeignetsten.
Da sie aber a priori nicht bekannt ist, legt man die Parameterwerte t_k durch die Distanzen der aufeinanderfolgenden Punkte so fest, dass gilt :
t_0 = 0 , t_k = t_(k-1) + √((x_k - x_(k-1)) ^ 2 +(y_k - y_(k-1)) ^ 2), k = 1,2, ..., n
Wie das ganz genau gemeint ist kannst du an dem Beispiel sehen, welches im Buch präsentiert wird, das ist mit Worten nicht so schön zu beschreiben.
Vielleicht bringt dich das weiter, vielleicht aber auch nicht, auf jeden Fall kann man aus dem Buch etwas lernen.
Hier mal ein Link, der zeigt welches Buch ich überhaupt meine ;
Vielleicht gibt es davon schon eine neuere Auflage als die 3-te,
Ich habe die 3-te Auflage des Buches auf reBuy für 3,29 € gesehen und auf Ebay für 4,96 €
Da kämen noch Versandkosten hinzu.
Wenn man also nicht übertrieben arm ist, dann kann man es auch einfach im Internet kaufen; das Buch lohnt sich auf jeden Fall.
An deiner Frage kritisieren muss ich, dass du nicht die Originalaufgabe als Bild hier rein gestellt hast, sondern nur ein Bild von einer Formel; ich finde deine Frage schwer zu verstehen; könnte aber auch an mir liegen.
das hat nun soweit geklappt, habe nur noch das Problem, dass Matlab bei den Übergangsstellen von Gerade und Kurve NaN (Not a number ausgibt)