Wie kann ich mit dem Sandwichkriterium beweisen, dass dies eine Nullfolge ist?
Nach unten abschätzen ist einfach, ich erhalte 1/(2^k ) ist kleiner als die genannte Folge und konvergiert gegen null. Ich brauche dann eine größere Reihe, die gegen 0 konvergiert. Was nimmt man und wie beweise ich es?
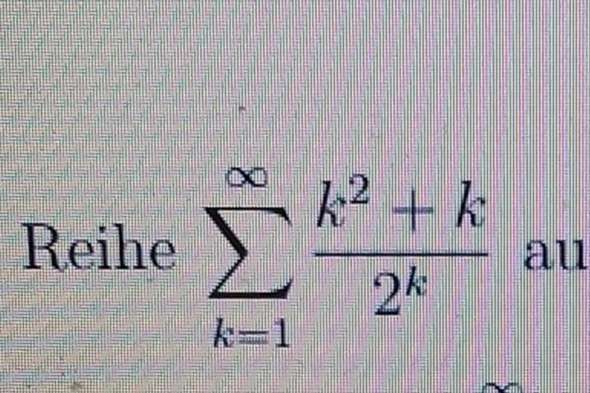
5 Antworten
Was mir sofort einfällt ist
2 k^2 / 2^k
Zu
k^2 / 2^k
siehe
https://duckduckgo.com/?q=beweis+konvergenz+k%5E2+%2F+2%5Ek&t=ffnt&ia=web
https://www.mathelounge.de/561570/konvergenzradius-k-2-x-2-k
Wenn ihr schon wisst, dass 2^k asymptotisch schneller wächst als k^2, kannst du das natürlich für den Beweis heranziehen - das ist äquivalent damit, dass der Quotient eine Nullfolge bildet.
Aber dass die Folgenelemente eine Nullfolge bilden, bedeutet noch lange nicht, dass die Reihe konvergiert - bekanntestes Gegenbeispiel ist die harmonische Reihe. Glücklicherweise konvergiert aber die Reihe mit den Folgegliedern k^2/2^k.
wo macht man sowas? Mathestudium?
f(x) = sum {k=1} x^k = x/(1-x), x < 1
f'(x) = = sum {k=1} k * x^(k-1) = x/(1-x)^2
f''(x) = = sum {k=1} k * (k-1) * x^(k-2) = -2/(x-1)^3
f''(x) = = sum {k=0} (k+1) * k * x^(k-1) = -2/(x-1)^3
x * f''(x) = sum {k=0} (k+1) * k * x^k = -2x/(x-1)^3
Setze x=1/2
sum {k=0} (k+1) * k * (1/2)^k = -2x/(x-1)^3 = 8
Der Index k=0 zählt nicht, denn (k+1)*k/2^k = 0 für k = 0
Weil die Summe gegen 8 konvergiert, muss (k+1) * k * (1/2)^k eine Nullfolge sein.
Du meinst die Folge ...
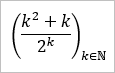
... der Summanden der Reihe, oder? (Denn die Reihe selbst konvergiert sicher nicht gegen 0.)
Wenn man nur zeigen soll, dass es eine Nullfolge ist, würde ich dafür nicht das Sandwich-Kriterium nutzen, sondern das anders zeigen. Aber da du konkret nach Sandwich-Kriterium gefragt hast ... Man könnte das beispielsweise folgendermaßen zeigen ...




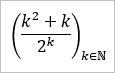




Wenn du nicht konkret nach Sandwich-Kriterium gefragt hättest, hätte ich das so gezeigt ...
https://i.imgur.com/W0fQZRM.png
Damit hätte man dann nicht nur gezeigt, dass die Folge eine Nullfolge ist, sondern auch, dass die entsprechende Reihe konvergiert.
Das ist keine Nullfolge! setze einfach mal die ersten Zahlen ein:
1+ 3/2 + 3/2 + 5/4 +15/16 +21/32 +28/64 ...., für mich tendiert sie gegen 7
Es geht nicht um das Konvergenzverhalten der Reihe, sondern um die der Folge.
_
danke, muss man noch nicht beweisen, dass 2 k^2 / 2^k gegen 0 konvegiert oder kann man einfach sagen, dass 2^k schneller wächst als der Zähler?