Konvergente oder Divergente Folge?
Hallo
Ich habe eine Folge mit lim n zu unendlich = -12
Eine Nullfolge ist, eine Folge, die gegen 0 konvergiert (sich annähert).
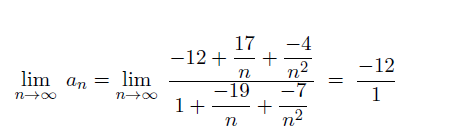
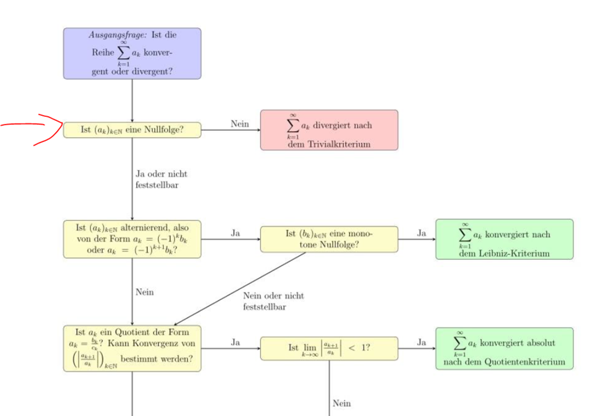
Jetzt frage ich mich ob mein Schema nicht geht (rot markierter Bereich) oder ich etwas falsch verstehe. Laut Schema würde sie divergieren nicht?
Schema:
1 Antwort
Redest du über die Reihe
oder über die Folge (a_n)?
Die Folge konvergiert, wie oben gezeigt, gegen -12. Die Reihe divergiert aber, da (a_n) keine Nullfolge ist. Also stimmt alles, was du schreibst.
Ganz so argumentieren kannst du aber nicht. Du summierst nicht unendlich oft -12 auf, sondern Zahlen die gegen -12 konvergieren. Das Problem ist, dass für eine Folge, die nicht gegen 0 konvergiert, das Cauchy-Kriterium verletzt ist.
Hier habe ich mich falsch ausgedrückt. Danke für die Korrektur.
Du hast natürlich recht. Die Folge konvergiert gegen -12, aber unendlich viele -12 gibt unendlich ^^