Wie kann ich ein absolutes Maximum durch eine Ableitungsfunktion erkennen?

Begründe, ob die Aussage wahr oder falsch ist:
f hat ein absolutes Maximum bei x = -1.
—> Falsch, bei x = -1 liegt ein abs. Minimum
Wie kann man das erkennen? Meine Begründung: Da bei NST in f‘(x) VZW von - nach + —> TIP in f(x). Aber woher soll ich jetzt wissen, dass es ein ABSOLUTER TIP ist? Muss ich dafür f(x) etwa skizzieren?
DANKE!
1 Antwort
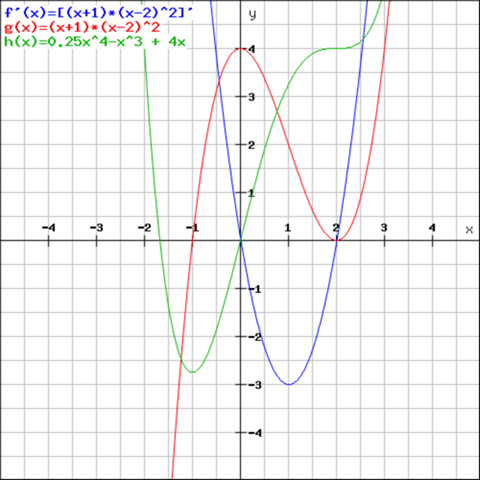
Hi Sarah,
in diesem Fall kann man argumentieren, dass es der einzige Tiefpunkt ist.
Der Graph der Ableitung ist ab dort (x = -1) nur noch positiv, also ist die Funktion für alle x > -1, streng monoton steigend.
Vermutlich hast Du auch bemerkt dass für x = 2, kein Extrempunkt vorliegt, da der Graph der Ableitung kein VZW hat, also haben wir hier einen Sattelpunkt. (Diese Anmerkung ist aber für die Behauptung dass bei x = -1 der absolute TP liegt, gar nicht unbedingt nötig, es reicht die Bemerkung dass die Funktion für alle x < -1 strecng monoton steigend ist, also kann sie weiter keinen TP haben.
LG,
Heni

Ja, das habe ich ja gesagt, bei x = 2 haben wir keinen Extrempunkt sondern einen Sattelpunkt (Terassenpunkt). Da ist zusätzlich f '(2) = 0 (also kein VZW), Das sieht man auch aus dem Graphen der ersten Ableitung. Das war ja auch der Hauptgrund meiner Argumentation, dass der Graph keine weiteren Extrempunkte hat als diesen einen TP bei -1. Und "ja", dieser Terassenpunkt ist ein Wendepunkt, aber kein Extrempunkt.
Könnte man auch den absoluten TIP sehen, indem man f(x) skizziert? Also wie würde dann der Graph aussehen? Ich kenne es nämlich nur so, dass man die Ableitungsfunktion skizziert.
Ich würde mich sehr über eine Antwort freuen!
Ja, hier kann ich leider nicht ein Bild posten. Ich schreibe Dir eine andere Antwort, wo ich den Grpahen der Funktion in grün dazu skiziere.
Nein, in der Hauptantwort füge ich ein Bild hinzu!
Vielen Dank für die Antwort!
Muss es aber nicht heißen: Die Funktion ist für x < -1 streng monoton FALLEND, also kann sie keinen weiteren TP haben.
Ja, auch richtig, aber das ist eigentlich eindeutig, klar kannst Du diese Bemerkung auch einbauen.
Also für x <= 1 ist die Ableitung negativ, also < 0, demnach kann es weiter keinen Extrempunkt geben (denn Extrempunkt - egal ob HP oder TP - kann ja nur dann vorliegen wenn die Ableitung = 0 ist.. Demnach ist für x € (-∞, -1 ) kein weiterer Tiefpunkt möglich (wohlgemerkt: dier Graph beginnt bei +∞ und fällt bis zu dem TP für x = -1) und dann aber ist die Bemerkung die ich oben gemacht habe ausschlaggebend. für den Verlauf des Graphen für x € (-1; +∞).
Dankeschön!
Kleine Frage noch: Aus der NEW-Regel geht hervor, dass die Extrempunkte der 1. Ableitung bzw. die Nullstellen der 2. Ableitung die Wendepunkte von f(x) beschreiben. Aber in Ihrem obigen Schaubild ist es ja kein WEP, sondern ein Terrassenpunkt. Wie soll man daraufkommen? (Mir ist klar, dass ein Terrassenpunkt ein besonderer Wendepunkt ist).