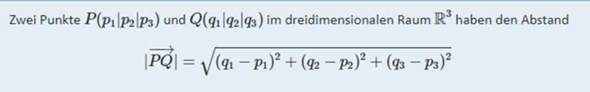Wie beweist man das C nicht auf der Strecke liegt?
A(2|1|-4)
B(6|1|-12)
C(0|1|0)
-Weise nach, dass der Punkt C auf der gerade g durch die Punkte AB, aber nicht auf der Strecke AB liegt
- Auf der Strecke AB gibt es einen Punkt D, der von B 3× soweit entfernt ist wie von A. Bestimme fie Koordinaten von D
Ich habe nur den ersten Teil von der erste Aufgabe gelöst und komme leider nicht weiter
3 Antworten
Es ist:
Zum Nachweis, dass C auf g liegt, setzen wir
und lösen komponentenweise nach λ auf. Es ergibt sich in allen Komponenten λ = -1/2. Damit liegt C auf g.
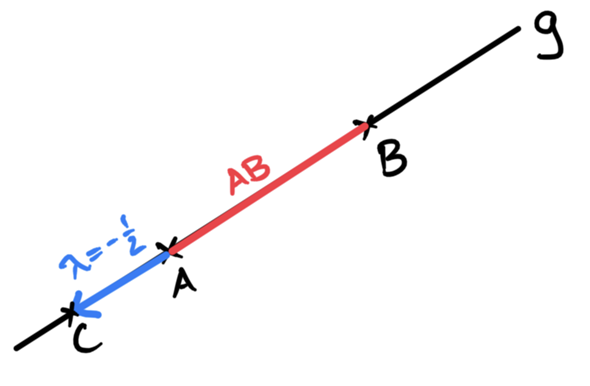
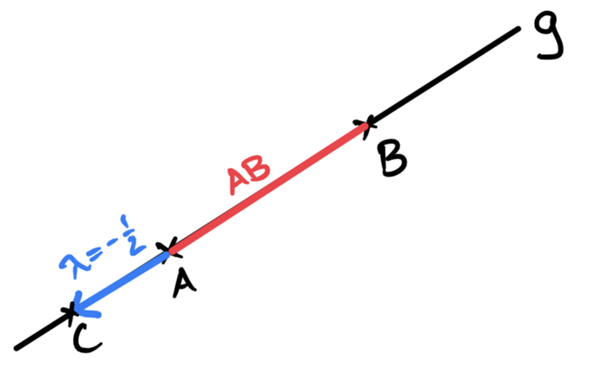
Die Strecke AB liegt zwischen A und B, wobei das der Teil von g ist, für den λ zwischen 0 und 1 liegt (für λ = 0 ergibt sich A, für λ = 1 ergibt sich B, für Werte dazwischen ergeben sich Punkte zwischen A und B, also auf der Strecke AB). Um C zu erreichen, muss allerdings λ = -1/2 gesetzt werden.
Für C geht man also von A entgegengesetzt der Richtung AB die halbe Strecke AB entlang. Der Punkt liegt also nicht zwischen A und B und damit nicht auf der Strecke AB.
Die y-Werte sind alle gleich, alle Punkte liegen also in der
y-Ebene und wir müssen nur die beiden anderen betrachten.
Wir haben
(6 | -12)
(2 | -4)
(0 | 0) liegt nicht zwischen (6 | -12) und (2 | -4), weil die Koordinaten
(0 | 0) nicht dazwischen liegen.
Bei Verringerung von x um 4 erhöht sich z um 8.
Also erhöht sich bei V. von x um 2 z um 4.
Dann wird aus (2 | -4) (0 | 0). Der Punkt liegt also auf der Geraden.
Hi,
da ist es am einfachsten zu beweisen dass der Abstand zwischen A un B nicht gleich ist mit der Summe der Abstände zwischen A und C bzw B und C
Den Abstand zweier Punkte im Raum berechnest Du mit der Formel:
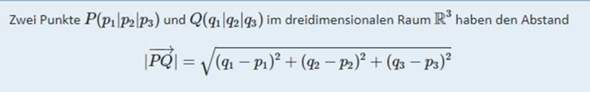
Hilft Dir das?
LG,
Heni