Wie berechne ich das hier (rekursive Folge)?
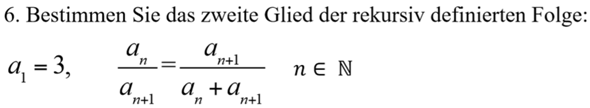
Ich komme anhand der Mitternachtsformel auf 1.845, aber laut Lösung wäre 4.854 richtig. Wie komme ich darauf?
3 Antworten
Hallo,
setze a(n+1)=x und a(n)=3, multipliziere über Kreuz, bring alles auf die Seite mit dem x² und wende die pq-Formel an.
Hat etwas mit dem Goldenen Schnitt zu tun.
Herzliche Grüße,
Willy
Ich ersetze die Variablennamen mal durch schönere um einfacher rechnen zu können:
a / b = b / (a + b) | * b
a = b ^ 2 / (a + b) | * (a + b)
a ^ 2 + a * b = b ^ 2
b ^ 2 - a * b - a ^ 2 = 0
pq-Formel:
b_1,2 = (1 / 2) * a ∓ √((1 / 4) * a ^ 2 + a ^ 2)
b_1,2 = (1 / 2) * a ∓ √(5 / 4) * a
Und mit a = 3 erhält man:
b_1= -1,8541
b_2 = 4,8541
Nun noch die Variablen zurück umbenennen:
a_2 = -1,8541
oder
a_2 = 4,8541
3/x = x/(3+x)
3*(3+x) = x*x
0 = x² - 3x - 9 ...............wie Mitternacht ? oder heißt pq so bei Euch ?
1.5 + - wurzel( 2.25 + 9)