Restklassen Wieso ist das so (Mathe)?

[4]5 ist [-1] oder [9] in der restklasse Z10 ist doch auch [-1]. Na wenn’s diesmal stimmt dann ist doch einfach ausgedrückt: wenn die Zahl in der Klammer eins kleiner ist als die Restklasse, dann ist das Ergebnis doch immer -1 oder?

habs von hier https://youtu.be/j8DXenS5h48?si=uQ2EicQr2jvcOzUr

Ab minute 27:35

hab nur seine Erklärung nicht verstanden

Comments

[jjsch5]

Bitte was?

[Todaboi]

Sorry hab mich vertan ,kompletter Denk Fehler ich meine z.b [4]5 ist [-1] oder [9] in der restklasse Z 10 ist doch auch [-1]. Na hoffentlich ist es jetzt richtig

Answer 1

[mihisu]

wieso ist dann 6 × 6 =-1

Das stimmt doch gar nicht! Bei den Restklassen modulo 7 ist NICHT [6 ⋅ 6]₇ = [-1]₇. Stattdessen ist [6 ⋅ 6]₇ = [1]₇.

$6\cdot 6=36$

Bei den Restklassen modulo 7 kann man nun Vielfache von 7 addieren oder subtrahieren und landet in der gleichen Restklasse...

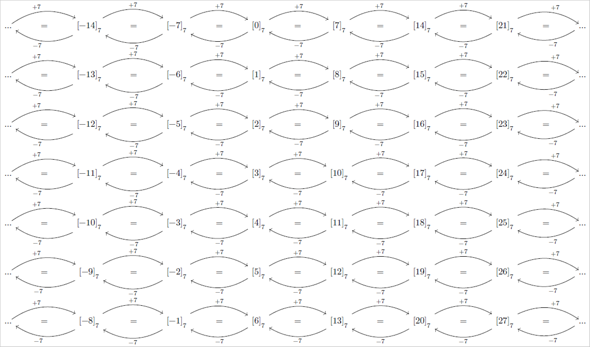
Das bedeutet dann insbesondere...

$[r+k\cdot 7]_7=[r]_7$

Im konkreten Fall kann man (indem man eine Division von 36 durch 7 mit Rest durchführt) erkennen...

$36 : 7=5\text{ Rest: }1$

Bzw. ...

$36 = 1+ 5\cdot 7$

Und damit erhält man dann...

$\left[36\right]_{7} = \left[1+ 5\cdot 7\right]_{7}=\left[1\right]_{7}$

Bzw. woher der Name RESTklasse auch stammt... Alle ganzen Zahlen, die bei Division durch 7 mit Rest den gleichen Rest r liefern, liegen in der gleichen Restklasse [r]₇. Und da 36 bei Division durch 7 den Rest 1 liefert, liegt 36 in der Restklasse [1]₇. Und dementsprechend ist dann [36]₇ = [1]₇.

=============

Bei [4 ⋅ 4]₅ kann man dann analog dazu...

$\left[4\cdot 4\right]_5=\left[16\right]_5=\left[1+3\cdot 5\right]_5=\left[1\right]_5$

... erkennen. (Bzw. kann man, nachdem man 4 ⋅ 4 = 16 berechnet hat auch schrittweise jeweils 5 subtrahieren, bis man bei 1 angekommen ist.)

============

Wenn ich richtig sehe, ist es doch immer die Restklasse -1 rechne und wenn ich diese Zahl mit sich selbst multipliziere kommt -1 raus.

Nein. Man erhält dann 1, nicht -1.

$\left[n-1\right]_{n}\cdot \left[n-1\right]_{n}=\left[-1\right]_{n}\cdot \left[-1\right]_{n}=\left[\left(-1\right)\cdot \left(-1\right)\right]_{n}=\left[1\right]_{n}$

Bzw. kann man das auch so sehen...

$\left[n-1\right]_{n}\cdot \left[n-1\right]_{n}$

$=\left[\left(n-1\right)\cdot \left(n-1\right)\right]_{n}$

$=\left[\left(n-1\right)^2\right]_{n}$

$=\left[n^2+2n+1\right]_{n}$

$\overset{\text{(*)}}{=}\left[1\right]_{2}$

Bemerkung zu (*): Da n² = n⋅n ein Vielfaches von n ist, ändert die Addition bzw. Subtraktion von n² bei Restklassen modulo n nichts. Da 2n ein Vielfaches von n ist, ändert die Addition bzw. Subtraktion von 2n bei Restklassen modulo n nichts.

Comments

[Todaboi]

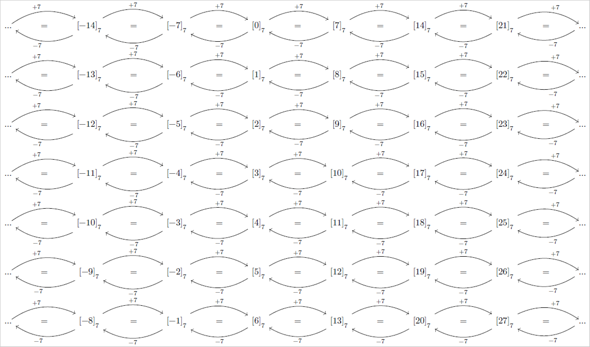
Danke für die ganze Mühe, die du hier reingesteckt hast. Nur hatte ich einen Denkfehler gehabt beziehungsweise falsch gedacht vielleicht jetzt in der Nachfrage, wenn’s dann da richtig ist. 😅

Answer 2

[FataMorgana2010]

Wenn du modulo m rechnest, dann ist

(m-1) * (m-1) = m² - 2m + 1 = 1

und nicht -1.

Deine Beispiele sind auch falsch: 6*6 = 36 und das modulo 7 ist 1, 4*4=16 und das Modulo 5 ist ebenfalls 1.