Kann mir jemand diese Aufgabe über Extrem- und Wendepunkte erklären?
Guten Abend,
ich habe zum Thema „Extrem- und Wendepunkte bestimmen“ noch drei fragen (diese befinden sich hinter den Aufzählungspunkten), um das Thema vollständig zu verstehen, vielleicht hat ja jemand Lust, mir dabei weiterzuhelfen. ✌️💪💚
Beispielaufgabe:Schaubilder f(x), f‘(x), f‘‘(x) und f‘‘‘(x):
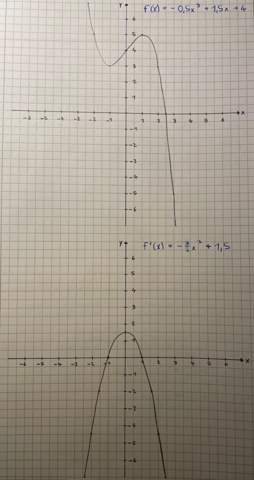
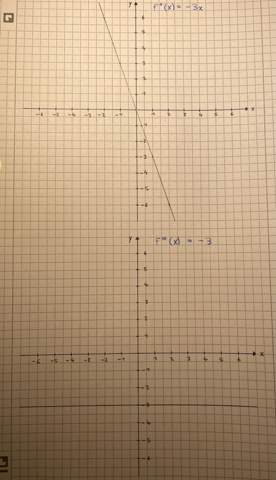

Extremstellen werden bei der ersten Ableitung Nullstellen, denn Hoch- und Tiefpunkte werden zu Nullstellen.
Das heißt, man setzt die erste Ableitung gleiche Null, um die x-Werte für die Extremstellen zu bekommen.
Folgendes verstehe ich noch nicht:
Die gefundenen x-Werte der Extremstellen werden in die zweite Ableitung eingesetzt, um zu bestimmen, ob es sich um einen Hoch- oder Tiefpunkt handelt. Ich verstehe, wie man es sich merkt, z.B. an dem Beispiel von Hamburger02:
Stell dir vor, du kommst mit dem Roller von links auf der x-Achse angerauscht. Dann machst du eine Linkskurve: die führt dich in die positiven y-Werte, also ist eine Linkskrümmung positiv bzw. f''>0: Linkskrümmung ist positiv
Wenn du eine Rechtskurve machst, fährst du in die negativen y-Werte: f'' < 0: Rechtskrümmung ist negativ.
Aber ich verstehe anhand des Diagramms der zweiten Ableitung, in das man die x-Werte der Extrempunkte einträgt, immer noch nicht, warum sich das Diagramm genau so verändert und warum man es dann dort so bestimmen kann.
Jetzt haben wir die Extremstellen und wissen, ob es sich um einen Hochpunkt oder einen Tiefpunkt handelt und müssen nur noch, um die Extrempunkte herauszufinden, die x-Werte der Extremstellen in die normale Funktion einsetzen.
Wendepunkte bestimmen:

Hier verwirrt mich zuerst auch, dass auf dem Foto unten bei den Krümmungswechsel-Varianten zuerst eine Wendestelle als x-Wert drinnen in der Klammer steht und dann zweimal eine Extremstelle. Ich denke, dass ist ein Fehler des Lehrers.
Wendestellen werden in der ersten Ableitung zu Extremstellen und in der zweiten Ableitung zu Nullstellen. Das heißt, man muss die zweite Ableitung gleich Null setzen, um die x-Werte für die Wendestellen zu erhalten.
Folgendes verstehe ich noch nicht:
Die gefundenen x-Werte der Wendestellen muss man jetzt in die dritte Ableitung einsetzen.
- Warum ändert sich das Schaubild der dritten Ableitung so, dass ich anhand dem Schaubild erkennen kann, ob es ein rechts-links-Krümmungswechsel ist, ein links-rechts-Krümmungswechsel ist, oder keine Aussage möglich ist, ob eine Wendestelle vorliegt?
- Was sind die oben genannten Krümmungswechsel bei der Berechnung des Wendepunktes am Schaubild genau?
Um die Wendepunkte zu bestimmen, muss man nun die x-Werte der Wendestellen in die normale Funktion einsetzen.
Vielen Dank für deine Hilfe 💪
3 Antworten
Aber ich verstehe es noch nicht anhand des Schaubildes der zweiten Ableitung, in welche Funktion man ja die x-Werte der Extremstellen einsetzen tut, warum sich das Schaubild genau so ändert und man es dort dann so bestimmen kann.
f'' gibt die Krümmung an. Wenn man mit x = -1 in das Schaubild dafür geht, liest man einen positiven y-Wert ab (+3). Daraus schließt man, dass bei dem Extremun bei x = -1 eine Linkskrümmung vorliegt. Daher muss bei -1 ein Tiefpunkt liegen. Diro bei x = +1. Da liest man im Graphen von f'' -3 ab: Rechtskrümmung: Hochpunkt. Am Wendepunkt von x = 0 ist f'' = 0, also geibt es da keine Krümmung: Wendepunkt. Man kann auch ablesen, dass bei diesem Wendepunkt die Krümmung von links auf rechts wechselt, da der Graph von f'' von positive auf negative Werte wechselt.
(Jetzt haben wir die Extremstellen und wissen, ob es sich um einen HP oder TP handelt und müssen nur noch, um die Extrempunkte herauszufinden, die x-Werte der Extremstellen in die normale Funktion einsetzen.)
Genau, um den zugehörigen Funkktionswert zu ermitteln und dann z.B, angeben zu können:
H(1/5); T(-1/3)
Warum ändert sich das Schaubild der dritten Ableitung so, dass ich anhand dem Schaubild erkennen kann, ob es ein rechts-links-Krümmungswechsel ist, ein links-rechts-Krümmungswechsel ist, oder keine Aussage möglich ist, ob eine Wendestelle vorliegt?
Interessant ist da nur noch das Vorzeichen, das hier konstant negativ ist. Bei Funktionen höheren Grades muss das aber nicht so sein, denn dann kann die Funktion auch meherer Wendestellen haben. Eselsbrücke: Das Vorzeichen der 3. Ableitung f'''entspricht dem Vorzeichen der Krümmung, mit der die Funktion ankommt, hier als mit links und dann haben wir einen Krümmungswechsel links-rechts. Keine Aussage aus f''' betreffs Krümmungswerchsel kann man ziehen, wenn es = 0 ist.
Was sind die oben genannten Krümmungswechsel bei der Berechnung des Wendepunktes am Schaubild genau?
Das sieht man am Graph von f(x) direkt: der kommt mit einer Linkskrümmung an und geht nach dem Wendepunkt mit einer Rechtskrümmung weiter. Hat man den Graphen von f(x), kann man das direkt sehen und braucht eigentlich gar nichts mehr zu berechnen. Hat man den Graphen nicht, muss man ihn halt berechnen.
Die Berechnung könnte man sich in der Praxis (leider nicht in der Klausur) auch dann sparen, wenn man weiß, dass links vom WP ein TP liegt, der immer eine Linkskrümmung hat und rechts davon ein HP liegt, der immer eine Rechtskrümmung hat.
Wenn ich aber nur die Extremstellen ausrechnen muss, muss ich dann nur die erste Ableitung, also f‘(x) = 0 setzen? Dann könnte es sich doch aber auch um einen Sattelpunkt handeln?
Richtig. Das kann aber erst bei Funktionen ab dem 3. Grad passieren. Bei einer vollständigen Kurvendiskussion in einer Klausur wird wahrscheinlich die Überprüfung mit f'' erwartet.
Muss ich dann auch noch laut der Aufgabenstellung die gefundenen Lösungen in die dritte Ableitung einsetzen, um den Krümmungswechsel zu bestimmen, oder um festzustellen, dass keine Aussage möglich ist, ob eine Wendestelle vorliegt?
Mit etwas Erfahrung kann man das so abschätzen aber auch hier wird in der Klausr sicherlich die vollständige Rechnung mit f''' ≠ 0 erwartet.
Wieso kann es sein, dass keine Aussage möglich ist, ob eine Wendestelle vorliegt?
Das ist relativ selten, kommt aber in der Regel dann vor, wenn die 3. Ableitung eine doppelte Nullstelle an der Wendestelle hat.
Beispiel:
f(x) = 1/60 x^5 - 1/12 x^4 + 1/6 x^3 - 1/6 x^2
f'' (x) = 1/3 x^3 - x^2 + x - 1/3
f''(1) = 0
f''''(x) = x^2 - 2x + 1 = (x - 1)^2
f'''(1) = 0
....und dennoch liegt bei x = 1 eine Wendestelle vor. Das kriegt man dann durch die Untersuchung des Krümmungswechselverhaltens raus, indem man eine Wert knapp über und einen knapp unter der Wendestelle einsetzt, z.B.
f''(0,9) = -0,0003
f''(1,1) = +0,0003
Die Krümmung wechselt als von rechts auf links.
...kannst du ja selber mal ausrechnen.
Ich habe mir einfach die Definitionen auswendig gelernt. Um sich zu merken wo es Nullstellen, Extremstellen und Wendepunkte gibt, habe ich dir eine Grafik erstellt:

Mit dieser Grafik kannst du herausfinden mit welcher Funktion oder Ableitung man Extrem- und Wendestellen von f herausfindet. Du kannst aber nicht herausfinden, ob es sich um einen Tief- oder Hochpunkt handelt oder wie die Wnedestelle gekrümmt ist. Das machst du eine Ableitung weiter.
Ob es sich bei dir um einen Hochpunkt oder Tiefpunkt handelt kannst du anhand deiner Bilder ablesen. Du hast einen Hochpunkt in f bei x = 1. Da die zweite Ableitung f''(x = 2) = - 3 also kleiner Null, hast du einen Hochpunkt. Dieses -3 kannst du auch ablesen bei dir. Deshalb ein Hochpunkt.

Also: Die 1. Ableitung gibt dir Auskunft über die Steigung der Funktion an entsprechender Stelle. Wenn die Steigung 0 ist, befindet sich dort offenbar ein Punkt an dem der Graph sich wieder wendet und in die andere Richtung weiterläuft.
Wir haben also einen (zumindest lokalen) Extremwert gefunden.
In der zweiten Ableitung können wir dann (bei einer Parabel) feststellen, ob es sich um einen Hoch- oder Tiefpunkt handelt.
Einfach zu merken war es für mich, in dem ich mir immer die Normalparabel vor Augen halten. Ich weiß, dass diese nach oben hin geöffnet ist und bei x=0 ihren Tiefpunkt hat.
f(x) = x²
f'(x) = 2x
f''(x) = 2
Entsprechend muss eine Zahl > 0 auf einen Tiefpunkt schließen und eine Zahl < 0 auf einen Hochpunkt.
Die zweite Ableitung ist sozusagen die Steigung der Steigung einer Funktion und gibt die Krümmung des Funktionsgraphen an. Wenn man es sich bildlich vorstellen möchte, dann gibt sie Auskunft darüber, ob der Graph sich im oder gegen den Uhrzeigersinn dreht.
Im Uhrzeigersinn -> die Kurve kommt von unten, erreicht ihr Maximum und dreht sich dann wieder Richtung negativer Zahlenraum -> das nennt man auch konkav und macht sich durch einen negativen Wert in der zweiten Ableitung bemerkbar.
Gegen den Uhrzeigersinn läuft es entsprechend genau andersrum. Das nennt man dann konvex und macht sich durch einen positiven Wert in der zweiten Ableitung bemerkbar.
Was die dritte Ableitung angeht, findest du viele wichtige Informationen z. B. hier:
https://www.touchdown-mathe.de/titel/wendepunkte-berechnen-mit-der-3-ableitung/
Wenn ich die Extrempunkte einer Funktion bestimmen möchte, muss ich ja zuerst f‘(x) = 0 setzen, gefundene Lösungen der Extremstellen in die zweite Ableitung einsetzen, um herauszufinden, ob ein Hoch- oder Tiefpunkt vorliegt. Dann die x-Werte der Extremstellen in die normale Funktion einsetzen, um die Extrempunkte herauszufinden.
Wenn ich aber nur die Extremstellen ausrechnen muss, muss ich dann nur die erste Ableitung, also f‘(x) = 0 setzen? Dann könnte es sich doch aber auch um einen Sattelpunkt handeln?
Wird durch das einsetzen der gefundenen Lösungen, die bei f‘(x) = 0 setzen herauskommen in die zweite Ableitung ein Sattelpunkt ausgeschlossen, bzw. wie erkennt man einen Sattelpunkt rein rechnerisch? Ist ein Sattelpunkt keine Extremstelle?
Wenn ich die Wendestelle bei einer Aufgabe bestimmen muss, dann muss ich ja die zweite Ableitung = 0 setzen.
Muss ich dann auch noch laut der Aufgabenstellung die gefundenen Lösungen in die dritte Ableitung einsetzen, um den Krümmungswechsel zu bestimmen, oder um festzustellen, dass keine Aussage möglich ist, ob eine Wendestelle vorliegt?
Wieso kann es sein, dass keine Aussage möglich ist, ob eine Wendestelle vorliegt?