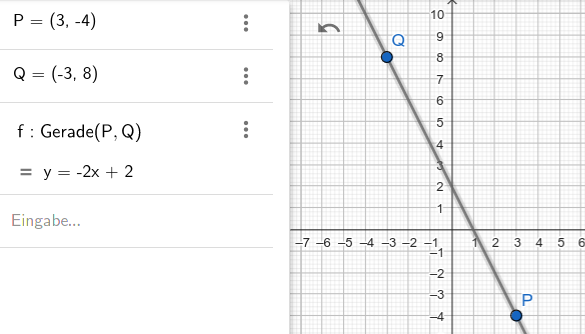
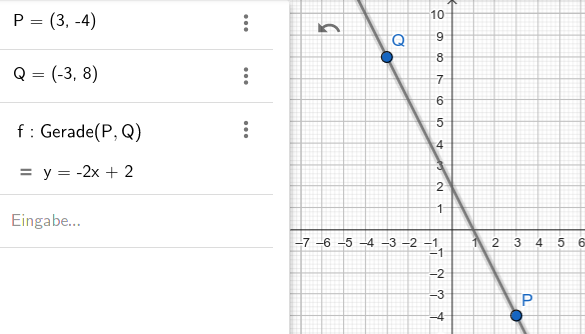
Wie berechnet man die Funktionsgleichung von den Punkten P (3/-4) und Q (-3/8)?
Wie berechnet man die Funktionsgleichung von den Punkten P (3/-4) und Q (-3/8)?
Und wie kann man den Funktionswert der Stelle x = 8 berechnen?
Geht es um eine lineare Funktion?
Ja
2 Antworten
soll es eine Gerade sein ?
.
Dann m = (8--4)/(-3-3) = 12/-6 = -2
Dann
8 = -2*-3 + b
2 = b
.
y = -2x + 2
x = 8 einsetzen
.
Bei einer Parabel müsste man von ax² + c ausgehen
oder ax² + bx
oder x² + bx + c
Wie berechnet man die Funktionsgleichung von den Punkten P (3/-4) und Q (-3/8)?
Überhaupt nicht. Punkte haben keine Funktionsgleichung. Punkte liegen auf dem Graphen von Funktionen, die durch eine Funktionsgleichung bestimmt sind. Wenn also, dann kann die Aufgabe lauten: Bestimmen Sie die Gleichung der Geraden, deren Graph durch die Punkte P (3/-4) und Q (-3/8) geht.
Also nehmen wir an, es soll sich um eine lineare Funktion handeln. Dann ist:
Die Steigung m ist mit den gegebenen Punkten:
Damit haben wir schon mal:
Fehlt noch "b", das mit den Koordinaten eines der beiden Punkte bestimmt werden kann (Ich wähle hier Q, hätte aber genauso gut P wählen können).
Damit
Skizze: