[Mathe] - Wie geht die Kettenregel?
Ich verstehe die Kettenregel leider noch nicht - vielleicht kann mir ja jemand dabei helfen, wie diese funktioniert und sie mir an 1-2 Beispielen (gelösten Aufgaben vom folgenden Bild) zeigen 💪 Vielen dank für deine Hilfe 💚

Wenn ich mir ein Video davon anschaue, dann fand ich es zu schnell gezeigt und habe es auch nicht wirklich verstanden.
Hat die Kettenregel etwas mit der h-Methode zu tun (die h-Methode kommt in der Arbeit nicht dran)?
Mit folgenden Buchstaben ist bei uns die Kettenregel im Buch vorgestellt:
innere Funktion: u(x)
äußere Funktion: h(u)
Kettenregel:
f‘(x) = h‘(u(x)) * u‘(x)
Merkregel:
„äußere mal innere Ableitung“
Ich habe folgende Beispielaufgaben (nicht von der Buchseite) verstanden:
f(x) = (3x+7)^(4)
innere Ableitung ist hier (3x+7) = 3
f‘(x) = 4(3x+7)^(3) * 3
f(x) = (x^(2) - 4)^(6)
innere Ableitung = 2x
f‘(x) = 6(x^(2) - 4)^(5) * 2x
Sowas wie e^(7x) verstehe ich immer noch nicht und Aufgaben mit Brüchen oder sogar Brüchen mit x in Sinus bzw. Kosinus bekomme ich auch nicht hin.
Wenn ein Minus oder Plus in einer Funktion steht wird hier auch nach der Summenregel verfahren bei der Kettenregel oder?
Das rechnerische ableiten habe ich so gut wie voll und ganz verstanden und schon sehr viele Übungsaufgaben gerechnet um es zu verinnerlichen 😅
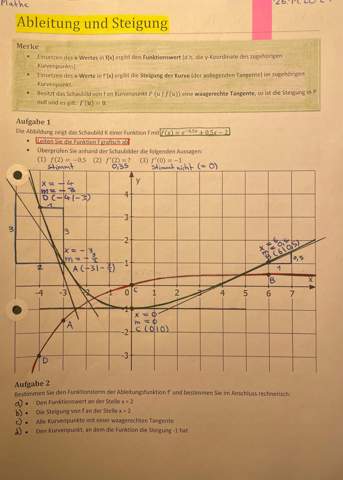
Beim Grafischem Ableiten verstehe ich, wie man eine Tangente zeichnet, m bestimmt und dann den x-Wert nimmt und den m-Wert als y-Wert, um den Punkt der abgeleiteten Funktion zu erhalten.
Die Aufgabe 1 habe ich ganz verstanden und bei der Aufgabe 2 habe ich a) und b) verstanden und auf dem 3. Bild berechnet, aber die Aufgabe c) verstehe ich nicht, wie man rechnerisch darauf kommt. 🤔
Bei der Rückseite habe ich die Aufgaben wenig bis garnicht verstanden, und es ist noch nicht vollständig berechnet


4 Antworten
Hat die Kettenregel etwas mit der h-Methode zu tun (die h-Methode kommt in der Arbeit nicht dran)?
Gleich mal die gute Nachricht und wie schon angekündigt: nein. Die h-Methode ist durch, jetzt wird richtig abgeleitet.
Ich verstehe die Kettenregel leider noch nicht -
Deswegen gucken wir nochmal kurz zurück und dann auf das neue Problem.
Bisher hatten wir ja nur Summen aus verschiedenen Potenzen. Das x stand solo da, höchstens mit einem Multiplikator davor und einer Potenz dahinter. Die Regel war: alte Hochzahl vorziehen, alte Hochzahl eins weniger.
So und nun guck dir mal die Aufgaben auf dem Blatt an. Da kommst du mit dieser Grundregel des Ableitens (und nur die hat mit der h-Methode zu tun) nicht so recht weiter. Da stehen noch andere Sachen um das x herum. Die Funktion ist sozusagen "verschachtelt", weshalb iich ja auch dafür wäre, statt von einer Kettenregel von einer Verschachtelungsregel zu sprechen. Die sogannte äußere Funktion ist die Schachtel und der Term, der das x enthält, ist der Inhalt bzw. die "innere Funktion".
Beispiele:
1a)
f(x) = 2e^3x
Da wäre 3x die innere Funktion und 2e^irgendwas wäre die äußere Funktion.
2c)
f(x) = 4 sin(5x)
innnere Funktion: 5x
äußere Funktion: 4sin
4f)
Das leitet man nach der Summenregel nacheinander ab.
-e^-5x
inner Funktion: 5x
äußere Funktion: -e^
-6e:
innere Funktion: gibts nicht
äußere Funktion: 6e
4e) das muss man erstmal ausklammern, dann Summenregel, dann hjeweils innere und äußere Funktion identifizieren.
So, nun kommen wir zur Kettenregel (also der Verschachtelungsregel):
Hat man eine Funktion, die aus einer inneren und einer äußeren Funktion besteht, leitet man die äußere und die innere Funktion getrennt ab und bildet dann das Produkt aus beiden. Kurzform: Äußere mal innere Ableitung
Beipiele:
1a) f(x) = 2e^3x
äußere Funktion u = 2e^3x, wobei wir 3x als Konstante betrachten.
u' = 2e^3x, denn e abgeleitet ergibt wieder e, da passiert gar nix.
inner Funktion v = 3x
v' = 3
also:
f'(x) = u' * v' = 2e^3x *3 = 6e^3x
h) f(x) = 2 - cos(0,5x)
Zuerst die Summenregel:
f'(x) = 0 + d/dx (-cos(0,5x))
d/dx (cos(0,5x)) leiten wir nun getrennt ab:
u = -cos (0,5x) (x wieder als Konstante betrachten)
u' = sin (0,5x)
v = 0,5x
v' = 0,5
f'(x) = sin (0,5x) * 0,5 = 0,5sin(0,5x)
Soll ich noch mehr Beispiele vorrechnen? Wenn ja, melden, denn jetzt ist mein Leberkäse fertig gebacken und es gibt Abendbrot.
Nur deine Gedanken die dir in der ersten Sekunde in den Kopf kommen, wie man die Aufgabe lösen kann, wenn du sie anschaust, z.B.: „Punkt einsetzen in f‘(x)“
Meinst du das? 🤔😅
Ich verstehe im Moment schon mal gar nicht das Problem, das du gerade hast. Gehst immer noch um Aufgabe 7? Die habe ich doch bereits gedeutet.
Ohh - Entschuldigung für die Verwirrung 😬 Habe oben nochmal eine Ergänzung zur Frage gemacht und da steht „Ergänzung nach 7 Tagen“. Es ist wirklich sehr unübersichtlich hier 😧
Ich glaube, ich solllte meine Kristallkugel mal wieder gründlich polieren....
Ich denke eher dass ich besser beschreiben sollte ;-) 🔮
Im Moment ist mir das zu anstrengend. Du kannst mich aber morgen gerne nochmal dran erinnern. Ab 5 abends bin ich aber nicht mehr da.
Natürlich - schönen Abend dir noch und genieß deinen Feierabend! 😊 Es ist absolut nicht selbstverständlich, du gibst dir einfach so viel Mühe hier… 💚
Ich habe die Aufgaben 1, 2, 3 und 4 bereits ganz gerechnet und denke, dass ich es verstanden habe 💪
Habe immer mal wieder die Seite https://www.ableitungsrechner.net/ benutzt, die du mir neulich empfohlen hast, um meine Ergebnisse zu überprüfen. 😊
Bei der Aufgabe 5 (Siehe Bild oben) habe ich Schwierigkeiten damit, da hier xe[-1;3] angegeben ist. Ich weiß nicht, was ich damit anfangen soll. 🤔
Ich würde, wenn diese Angabe nicht da wäre, einfach die Funktion ableiten und in die abgeleitete Funktion die angegebenen Werte einsetzen, um das Ergebnis der abgeleiteten Funktion für diese zu bestimmen.
Habe immer mal wieder die Seite https://www.ableitungsrechner.net/ benutzt, die du mir neulich empfohlen hast, um meine Ergebnisse zu überprüfen. 😊
Der ist echt klasse. Damit überrpüfe ich auch meine Ergebnisse. Passiert ja doch immer mal wieder ein Flüchtigkeitsfehler.
Ich weiß nicht, was ich damit anfangen soll.
Das weiß ich auch nicht, was das soll. Das könnte damit zusammenhängen, dass die Funktionen von sin und cos eigentlich immer nur von -2pi bis +2pi definiert wird, weil außerhalb dieses Intervalles die periodischen Wiederholungen kommen.
Ich würde, wenn diese Angabe nicht da wäre, einfach die Funktion ableiten und in die abgeleitete Funktion die angegebenen Werte einsetzen, um das Ergebnis der abgeleiteten Funktion für diese zu bestimmen.
Das würde ich auch machen.
Vielen Dank dir für deine Zeit und super verständliche Hilfe! 💚😊
Hatte ja neulich schon mal geschrieben, dass ich die ganze Ableiterei und später die folgende Kurvendiskussion immer klasse fand. Das muss man nur einmal richtig verstehen und dann nicht mehr viel lernen, weil es immer nur Wiederholung derselben Methoden ist.
Kannst du mir bei einer sehr einfachen Frage weiterhelfen? 😅😊
“Gegeben ist die Funktion f mit „f(x) = e^(x) + 3e^(-x)“;xeR. Welcher der drei Ableitungswerte f‘(0); f‘(1); f‘(-1) ist der größte?“
Ich habe die Werte in die Ableitung, die ich zuvor ausgerechnet habe, eingesetzt und folgendes erhalten:
f‘(0) = -2
f‘(1) = 1,61
f‘(-1) = -7,79
Ist hier der größte positive Wert (f’(1) =1,61) gemeint oder die -7,79?
Ohne Zusatz ist die größte Zahl immer die, die am weitesten rechts auf dem Zahlenstrahl liegt, also 1,61.
Ansonsten hätte nach dem höchsten Betrag gefragt werden müssen, wenn die -7,79 die Lösung hätte sein sollen.
Vielen Dank für deine extrem schnelle Antwort 🙏
Oben in dem Beitrag auf dem Foto bei der Aufgabe 7 habe ich alle 3 Berechnungen gemacht und habe nun alle 3 Werte und muss diese noch interpretieren. Kannst du mir da einen Tipp geben?
Meine Ergebnisse:
T‘(0) = -7/3
T‘(20) = -0,86
T‘(100) = 0,003
Mit zunehmender Zeit wird der Temperaturunterschied immer geringer und umso weniger Wärme fließt. Dementsprechend kühlt der Körper immer langsamer ab, je mehr sich seine Temperatur der Temperatur der Umgebung annähert. Die Temperaturkurve wird daher mit zunehmender Zeit immer flacher und nähert sich asymptotisch der Umgebungstemperatur.
Nur am Anfang schreibt man dann so wie du hin, wie man mit der inneren und äußeren Ableitung vorgeht, um es zu verstehen, oder?
u' = sin (0,5x)
v = 0,5x
v' = 0,5
Genau. Habe das wegen des (hoffentlich) leichteren Verständnisses in diese Einzelschritte zerlegt. Wenn man in der Kettenregel sicher ist, spart man sich die einzelnen Ziwschenschritte im Allgemeinen. Diese hinzuschreiben ist aber kein Fehler.
Das nervige finde ich immer, dass manche Bücher (mein Matheschulbuch z.B.) oft andere Buchstaben haben als es auf YouTube erklärt wird, oder wie hier von dir. Die Buchstaben sind ja eigentlich egal, welche es sind und es gibt leider keine immer einheitlichen Buchstaben - das ist bei Mathe echt manchmal verwirrend.
Wir haben für die innere Funktion u(x) und für die äußere Funktion h(u).
Da kommt man immer etwas mehr durcheinander - z.B. hast du ja nur die Buchstaben geschrieben, und im Buch steht dahinter in Klammern noch etwas , u(x); h(u). Das, was in den Klammern hier steht, verstehe ich nicht so wirklich, die Unterschiede von Buch und YouTube Erklärungen sind deswegen auch oft ein wenig verwirrend. 🤔
Ich könnte also auch einfach nur „u“ (innere Funktion) und nur „h“ (äußere Funktion) schreiben, oder?
Die Kettenregel ist nötig, wenn im abzuleitenden Funktionsterm ein weiterer Funktionsterm steckt. Typisches Merkmal ist, dass das x innerhalb der abzuleitenden Funktion (z. B. e-Funktion, sin-, cos-, tan-, Wurzelfunktion) nicht als "einfaches" vorkommt.
1a) hier musst Du die e-Funktion ableiten, brauchst also die Ableitungsregel um e^x abzuleiten; nur hast Du es hier nicht mit e^x, sondern mit e^(3x) zu tun, d. h. dieses 3x ist quasi ein weiterer Funktionsterm innerhalb der e-Funktion.
Die Ableitungsregel, die in Deiner Formelsammlung steht, gibt als Ableitung von f(x)=e^x an: f'(x)=e^x, also dasselbe. Das verleitet dazu zu glauben, dass e^"irgendwas" abgeleitet immer e^"irgendwas" ergibt. Tatsächlich muss man aber hier die Kettenregel anwenden, d. h. man muss dieses "irgendwas" ebenfalls ableiten und zu dem, was man mit der Ableitungsregel abgeleitet hat hinzumultiplizieren.
D. h. e^(3x) ergibt abgeleitet dieses e^(3x) (unverändert) mal der "inneren Ableitung", also der Ableitung des Exponenten, also mal 3.
Somit ist die Ableitung von f(x)=2e^(3x): f'(x)=2e^(3x)*3=6e^(3x). Vorne die 2 ist "nur" ein konstanter Faktor, der bekanntlich beim Ableiten beibehalten wird.
b) und c) gehen genauso, jeweils den Exponenten noch ableiten und hinten dran multiplizieren
d) hier hast Du es statt mit sin(x) mit sin(3x) zu tun, d. h. Du musst nicht nur den sinus ableiten, sondern auch noch die "innere Funktion" 3x, also:
f'(x)=3/2 * cos(3x) * 3 = 9/2cos(3x)
Warum ist die innere Ableitung nicht immer das was in den Klammern steht bzw. das was in der Basis steht sondern manchmal auch das, was im Exponent steht, z.B. bei „e^(3x)“?
Wie kann ich dann unterscheiden bei z.B.
f(x) = (x^(2) - 4) ^(6)
UND z.B.
f(x) = e^(3x)
ist was die innere und was die äußere Basis ist?
Die Kettenregel wird ja angewendet, wenn man Funktionsterme in der Form f(x)=g(h(x)) hat => f'(x)=g'(h(x)) * h'(x)
"Eigentlich" kann man jede Funktion in äußere und innere Funktion benennen, egal ob Potenzfunktion, Wurzelfunktion, e-Funktion, usw.
Das "Problem" bei den Ableitungsregeln ist, dass die innere Ableitung nicht erkennbar ist, wenn die innere Funktion "nur" das x ist. Ein Beispiel habe ich ja genannt: Die Ableitung von z. B. e^x ist wieder e^x; evtl. würde es klarer werden, wenn da e^x * 1 in den Sammlungen stehen würde (mit "* 1" für die innere Ableitung); ähnlich dann z. B. (sin(x))'=cos(x) * 1 oder (Wurzel(x))'=1/(2Wurzel(x)) * 1 [aber das würde wahrscheinlich den Rahmen der Formelsammlungen sprengen...].
Bei Deinem neuen Beispiel (x²-4)^6 hast Du die gesamte Potenz als äußere Funktion, die Du mit der Potenzregel ableitest, die Basis dieser Potenz (=x²-4) stellt die innere Funktion dar, d. h. die Ableitung davon ist dann: 6 * (x²-4)^5 * 2x = ...
Nach meiner obigen Ausführung könnte man "übertrieben geschrieben" auch die Potenzregel "erweitern": f(x)=x^n => f'(x)=n * x^(n-1) *1 ['*1'=innere Ableitung der Basis]
Aufgabe 4)
f(x) = e^(-0.5x) + 0,5x - 2
f(-2) = e^(1) - 1 - 2 = e - 3 = -0,282
P(-2/- 0,282)
f'(x) = -0,5e^(-0,5x) + 0,5
f'(-2) = -0,5 * e^1 + 0,5 = -0,86
Tangentengleichung T:
Ansatz:
T: y = mx + b
m = -0,86
y = -0,86x + b
P einsetzen:
- 0,282 =-0,86(-2) + b
b = -0,282 - 1,72 = -2,002 ≈ -2
T: y = -0,86 x - 2
Normalengleichung N:
Ansatz:
N: y = mx + b
m = -1 / -0,86 = 1,163
P einsetzen:
-0,282 = 1,163 * (-2) + b
b = -0,282 + 2,326 = 2,044
N: y = 1,163x + 2,044
Und so sieht das im Graphen aus:
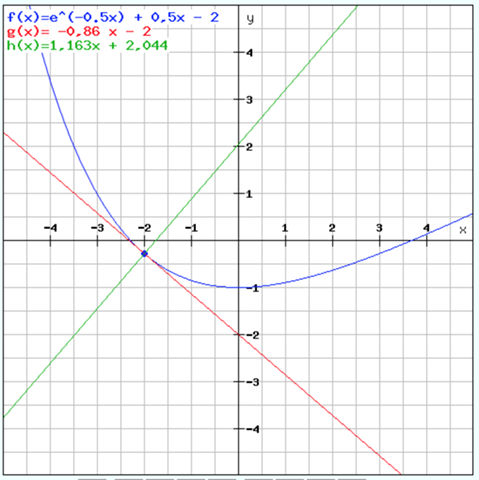
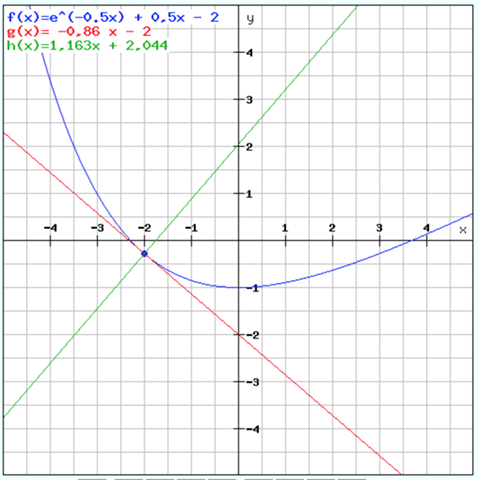
Hammermäßig - ich hab es ganz verstanden!!! ;-)
Kann mir so leichter merken, wie man von der Tangente die normale bildet:
mt * mn = -1
und dann einfach auflösen, in Gleichung einsetzen und erneut die Punktprobe machen, wie du sie auch gemacht hast 💪
Kann mir so leichter merken, wie man von der Tangente die normale bildet:
mt * mn = -1
Das ist dem Esel völlig egal, über welche Brücke er geht. ;-)
Die Aufgabe 2 kann leicht missverstanden werden. Es soll der Funktionsterm der Ableitung ermittelt werden und bezogen auf diese neue Funktion beziehen sich m.E. die folgenden Aufgaben a bis d. Kann aber auch anders sein.
Damit man mit den Funktionstermen nicht durcheinanderkommt, sollte man entweder konsequent weiter f' verwenden oder noch besser eine neue Funktion schreiben:
g(x) = f'(x) = -0,5e^(-0,5x) + 0,5
a)
g(2) = -0,5e^(-0,5*2) + 0,5 = -0,5/e + 0,5 = 0,316
Und nun stelle ich fest, dass in Aufgabe b) f(x) erwähnt wird, womit deine Betrachtung korrekt wäre.
Demnach:
f(2) = -0,632
b)
f'(2) = -0,5e^(-0,5*2) + 0,5 = -0,5/e + 0,5 = 0,316
c)bisher war es immer so, dass ein bestimmtes x vorgegeben war und an dieser Stelle f' bestimmt werden sollte. Jetzt geht es andersrum: eine Steigung wird vorgegeben und die zugehörigen x sind gesucht. So rum kann das ziemlich tricky werden und ist oft nur durch Näherungsverfahren zu lösen.
Waagrechte Tangente bedeutet:
f'(x) = 0
Also setzen wir an:
f'(x) = -0,5e^(-0,5x) + 0,5 = 0
0,5e^(-0,5x) = 0,5
e^(-0,5x) = 1
Um einen Exponenten von e wegzukriegen, wendet man den ln an:
ln e^(-0,5x) = ln 1
-0,5x * ln e = ln 1
-0,5x = ln 1
x = -2ln 1 = -2 * 0 = 0
Es gibt also nur eine Lösung und damit nur einen Kurvenpunkt mit waagrechter Tangente bei x = 0
d)
Ansatz:
f'(x) = -1
-0,5e^(-0,5x) + 0,5 = -1
-0,5e^(-0,5x) = -1,5
e^(-0,5x) = 3
ln (e^(-0,5x)= ln (3)
-0,5x = ln 3
x = -2 * ln 3 = -2,20
Das stimmt auch mit der Grafik überein.
Nur nebenbei: um zu einer gegebenen Steigung das x zu erhalten, sind die typischen Anwendungen: pq-Formel, Logarithmus, Polynomdivision, schätzen und rechnen und verbessert schätzen, grafische Lösung mit Funktionenplotter.
Muss man bei c) auch noch die Lösung x=0 in die normale Funktion einsetzen, um den x-Wert zu erhalten um so einen Punkt als Ergebnis für die Aufgabe 2 c) angeben zu können oder reicht als Lösung x = 0 aus?
*Frage gilt auch für die Aufgabe 2 d)
Hab alles verstanden wie du es erklärt hast, Hammer, nur die Frage von oben, da bin ich mir noch unsicher 🤔💚
Das Wochenende wird hart, nächste Woche 4 Klassenarbeiten, darunter auch Mathe am Freitag nächste Woche. Ganzes Wochenende durchlernen und dann schaffe ich das auch 💪
Hast du die Tage noch Lust mir auf der Rückseite zu helfen, da verstehe ich noch keine der Aufgaben so richtig 🤔 Oft schreiben die Lehrer anders auf als man es selber tun würde und man versteht es dann nur durch eine andere Schreibweise schlechter und ist am verzweifeln…
(hab es nicht selber gerechnet und die Aufgabe 4 ist noch unvollständig)
Ich habe dir genauso viel zu verdanken wie meinem Fleiß, mit dem ich dieses Schuljahr einfach so gut wie noch nie durchziehe 💪 Du hilfst mir so unglaublich viel weiter…
Muss man bei c) auch noch die Lösung x=0 in die normale Funktion einsetzen, um den x-Wert zu erhalten um so einen Punkt als Ergebnis für die Aufgabe 2 c) angeben zu können oder reicht als Lösung x = 0 aus?
Hmm, gute Frage. Die Frage nach einem Kurvenpunkt könnte man aber tatsächlich so interpretieren, dass es nur für eine Lösung P(x/f(x)) die volle Punktzahl gibt.
Ich habe dir genauso viel zu verdanken wie meinem Fleiß, mit dem ich dieses Schuljahr einfach so gut wie noch nie durchziehe
Danke und das freut mich. Das erinnert mich an meine eigene Schulzeit. War immer ein ziemlich fauler Schüler und bin manchmal nuur knapp am Durchfallen vorbeigeschrammt, was mit einer 6 in Latein (das muss man erstmal schaffen, eine 4 und der Schnitt ist hin) und Englisch 5 passieren kann. Konnte es aber immer gerade noch so mit Mathe und Physik ausgleichen. Habe dann aber die Kurve gekriegt und 1 Jahr vor dem Abi angefangen, mich richtig heftig reinzuknien, um dann am Ende noch ein Abi mit Auszeichnung zu schaffen.
Hast du die Tage noch Lust mir auf der Rückseite zu helfen, da verstehe ich noch keine der Aufgaben so richtig
Ok, ich schaus mir mal an.
Hast du Lust mir bei der Ergänzung von der Frage eine kleine Hilfe zur Lösungsweise geben? 😬