Lässt sich die Betragsfunktion f(x) = x*|x| an der Stelle x = 0 ableiten?
Ich weiß dass sich f(x) = |x| an der Stelle x=0 nicht ableiten lässt, bin mir aber nicht sicher wie das bei f(x) = x*|x| aussieht.
Danke im Voraus!
5 Antworten
Also wenn man die Funktion zeichnet, kommt sowas wie ne x^3-Funktion raus, nur eben mit quadratischen Werten:
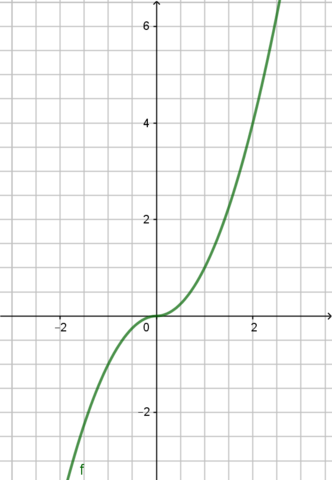
Demzufolge müsste da f'(0)=0 gelten und die Funktion differenzierbar, da eindeutig linear approximierbar, sein.
Letztendlich ist ja
f(x)=-x^2 für x<0
0 für x=0
x^2 für x>0
Das heißt
f'(x)=-2x für x<0
0 für x=0
2x für x>0
Und damit sind sowohl der links- als auch der rechtsseitige Grenzwert für x->0 dann 0.
Die Zeichnung ist praktisch die Anschauung dazu, das unten der formale Beweis.
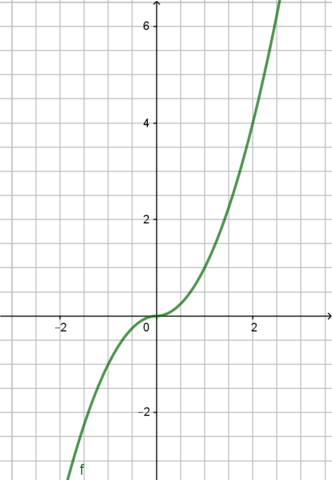
Ich hab dir doch oben die Funktion gezeichnet für x*|x|, wo soll die denn nen Knick haben? Der Unterschied ist ganz einfach der: da |x| im Prinzip ne lineare Funktion ist, hast du in der Ableitung keine Variable mehr. Bei x*|x| aber eben schon. Wenn du dann da x=0 einsetzt, wird das von beiden Seiten her 0, egal ob das Vorzeichen in der Ableitung positiv oder negativ ist. Und damit ist der Grenzwert eben eindeutig, weil von beiden Seiten aus gleich, was bei |x| nicht der Fall ist.
Es gilt
für alle x. Das lässt sich ableiten und ergibt an der Stelle x=0 f'=0
Du kannst die Funktion von rechts betrachten => f_R(x)=x^2 => f'_R(x)=2x.
Du kannst die Funktion von links betrachten => f_L(x)=-x^2 => f'_L(x)=-2x
Im Punkt x=0 stimmen damit beide Ableitung überein => die Ableitung existiert in diesem Punkt und beträgt f'(0)=0.
Noch eine kurze Frage zu dem Beispiel: beim Differentialquotient der beiden Grenzwerte bekomme ich X bzw. -X als ergebnis anstatt 2X und -2X.
Ich rechne dafür nach der formel (f(x)-f(0))/(x-x0) also (x^2-0)/(x-0).
Die Ableitung müsste ja lauten 2X und nicht X kann mir hier bitte noch jemand helfen wo der Fehler liegt?
Du darfst hier ja nicht durch x teilen, wenn x gegen 0 gehen soll. Sonst würdest du ja durch 0 teilen. Du musst erst den Differentialquotienten bestimmen und dann den Wert einsetzen.
Also (x^2-x0^2)/(x-x0)=[(x+x0)(x-x0)](x-x0)=x+x0.
Und dann kannst du x gegen x0 gehen lassen, dann kommt 2x0 raus. Und für 0 ist das dann eben die besagten 0.
Also der linksseitige und der rechtsseitige Grenzwert des Differenzenquotienten existieren und sie sie sind identisch. Folglich müsste die Funktion dort ableitbar sein.
https://www.wolframalpha.com/input/?i=lim+(x*%7Cx%7C)%2Fx+for+x+to+0%2B
Hey Danke für deine Antwort.
Was mir noch immer nicht ganz klar ist, wo der Unterschied zwischen den beiden Funktionen x*|x| und |x| liegt. denn sowohl die Ableitung als auch die ableitbarkeit an der Stelle x=0 unterscheiden sich bei beiden obwohl die Funktionen doch gleich aussehen (beide haben die für Betragsfunktion typische V-Form mit knick an der Stelle x=0)