Koordinaten berechnen?
Hallo, ich bekomme leider diese Aufgabe nicht hin. Es gibt zwei Punkte in dem Koordinatensystem. Diese sind A(2/2/2) und B (3/4/2). Diese bilden den Vektor AB, der die Seite eines Quadrats sein soll. Der Vektor AB ist parallel zur xy-Ebene.
Ich habe den Vektor AB berechnet und komme auf ( 1/2/0). Weiß aber nicht, wie ich jetzt nun vorgehen soll.
Ich muss die Koordinaten der zwei weiteren Punkte C und D berechnen
3 Antworten
Also wenn das die komplette Aufgabenstellung ist ist sie meines erachtens nicht eindeutig lösbar.
Wenn ich eine Seite eines quadrates im 3 Dimensionalen Raum habe kann ich diese eine Seite zu unendlich vielen Quadraten vervollständigen.
Es fehlen hier also noch angaben welche das eineutig machen.
Falls du nur ein mögliches Quadrat finden sollst. Rechne einfach im Zweidimensionalen Raum und gibt für alle Punkte z=0 vor, dann wirds einfacher.
Weiß aber nicht, wie ich jetzt nun vorgehen soll.
Zunächst legst du mal fest, dass das gesamte Quadrat parallel zu x-y-Ebene liegen soll, womit auch C und D die z-Koordinate 2 haben.
Nun definieren wir den Punkt C:
C(xc / yc / 2)
Und haben zwie Bedingungen, womit die zwei Unbekannten xc und yc lösbar sind:
1) AB und BC stehen stehen senkrecht aufeinander, also ist das Skalarprodukt = 0.
BC = (xc -3 / yc - 4 / 0)
AB * BC = 0 =
(xc - 3) + 2(yc - 4) + 0
2) AB und BC sind gleichlang:
(xc - 3)^2 + (yc - 4)^2 = 5
Die beiden Gleichungen muss man nun lösen.
_____________________________________________________________
Und hier die ganz einfache Lösung mit Hilfe einer Skizze:
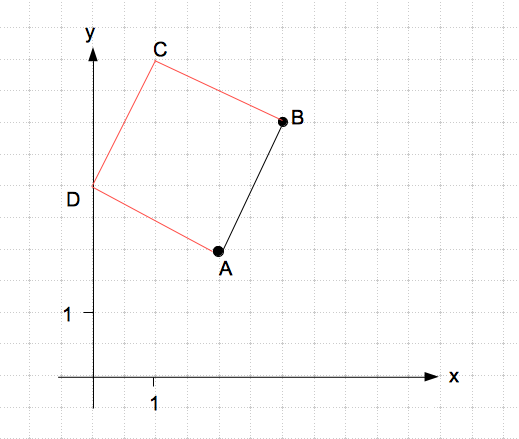
Gegeben A und B (schwarz).
Von A zu B geht es um 1 nach rechts und 2 nach oben. Senkrecht dazu geht es dann 1 nach oben und 2 nach links (rot)
Grundlage: zwei Geraden in der Ebene sind dann senkrecht wenn gilt:
m1 * m2 = -1
bzw.
m2 = -1 / m1
Ebenso kommt man von B auf C und liest die Koordinaten ab.
Daher:
C(1/5/2)
D(0/3/2)
Ah ja. Eine ganz einfache Lösung siehe oben als Ergänzung.
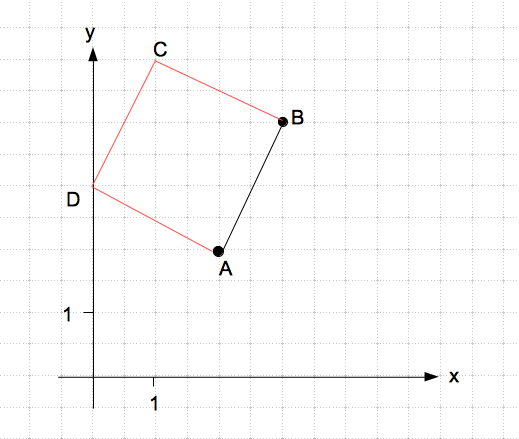
Gegeben sind die Punkte A(2/2/2) und B(3/4/2), die den Vektor AB bilden, der parallel zur xy-Ebene verläuft und die Seite eines Quadrats darstellt. Der berechnete Vektor AB ist (1/2/0). Nun müssen die Koordinaten der anderen beiden Punkte C und D berechnet werden, um das Quadrat zu vervollständigen.
Um die Koordinaten der Punkte C und D zu berechnen, musst du einen Vektor bestimmen, der senkrecht zum Vektor AB verläuft. Dies kannst du mit dem Kreuzprodukt von AB und dem Einheitsvektor der z-Achse tun. Addiere dann den berechneten Vektor zum Punkt B, um den Punkt C zu erhalten, und subtrahiere den berechneten Vektor von Punkt B, um den Punkt D zu erhalten. So hast du die Koordinaten aller vier Eckpunkte des Quadrats.
Danke dir, aber denke nicht, dass das der richtige Lösungsweg ist. Die Aufgabe ist in dem Teil ohne Hilfsmittel und für die Lösung gibt es nur 2 Punkte. Die Antwort müsste demnach sehr einfach sein.