Kartesisches Koordinatensysteme ein Punkt mehrere Koordinaten?
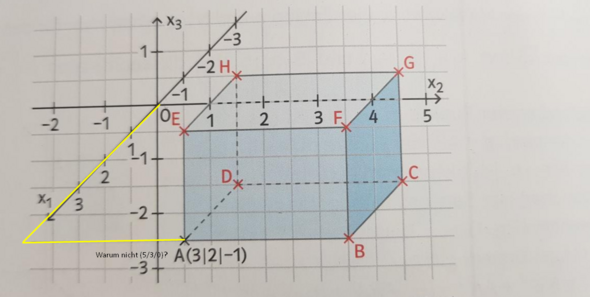
Wir haben die Hausaufgabe bekommen, uns das kartesische Koordinatensystem beizubringen. Die Grundlagen habe ich verstanden. Nur gibt es bei dem Quadrat für den Punkt A zwei oder sogar mehrere Koordinaten, die diesen angeben. Kann mir jemand erklären wie man auf die richtige Lösung kommt?
8 Antworten
A hat genau einen Punkt. Allerdings hat der Punkt eben 3 Koordinaten.
ein punkt P=(1,2,3) sagt dir bspw. aus:
wenn du beim ursprung startest, 1 in x-richtung gehst, 2 in y richtung und 3 in z richtung, dann gelangst du an den Punkt P.
Insofern gehören alle 3 koordinaten zum Punkt P.
Im Alltag bedeuten die 3 Koordinaten bspw. 1 Schritt nach vorne, 2 Schritte nach rechts und 3 Schritte nach "oben".
so ungefähr.
Du musst für jeden Punkt jeden seiner Koordinaten einzeln ablesen.
Du hast die Aufgabe ja nicht beschrieben. Es sieht so aus, dass die Koordinaten für A gegeben sind und Du die Koordinaten für die anderen Punkte bestimmen sollst. Und wenn A (3,2,-1) ist, ist D (2,2,-1).
Wäre A nicht vorgegeben, gäbe es in der Tat unendlich viele Möglichkeiten, u.a. auch Deine Lösung (5,3,0)
"Du hast die Aufgabe ja nicht beschrieben. Es sieht so aus, dass die Koordinaten für A gegeben sind und Du die Koordinaten für die anderen Punkte bestimmen sollst. Und wenn A (3,2,-1) ist, ist D (2,2,-1)."
Tatsächlich ist die eigentliche Aufgabe überhaupt nicht durch die Zeichnung allein und durch die Angabe der Koordinaten des Punktes A bestimmt.
Es müsste z.B. noch zusätzlich gesagt werden, dass es sich bei dem Körper ABCDEFGH um einen Quader mit lauter Seitenkanten parallel zu den Koordinatenachsen handeln soll. Andernfalls kann man sich eine unendliche Vielfalt von möglichen Lösungskörpern vorstellen, von welchen nur wenige tatsächlich Spatkörper oder sogar Quader sind.
Du hast 3 Achsen eingezeichnet: x1, x2 und x3.
A(3|2|-1) bedeutet:
du gehts in postiver x1 Richtung 3 Einheiten
du gehst in positiver x2-Richtung 2 Einheiten
du gehst in negativet x3-Richtung 1 Einheit
(Im Raum ist dies eindeutig, hier durch die 2D- Projektion scheint es so, als gäbe es mehrere Möglichkeiten)
Deswegen sage ich ja:
Im Raum ist dies eindeutig, hier durch die 2D- Projektion scheint es so, als gäbe es mehrere Möglichkeiten
Gerade wegen dieser Mehrdeutigkeit ist der Punkt A ja angegeben.
Wenn man nun unterstellt, dass das Gebilde ein Quader ist, ergeben sich die anderen Punkt aufgrund von A eindeutig.
Es ist richtig A könnte auch bei (5/3/0) liegen - aber wie gesagt: das ist die Angabe und die musst du akzeptieren. (Es ist so, als ob gegeben ist m = 5, kannst du auch nicht einfach sagen "ja, aber ich rechne lieber mit m=3")
Ich versteh dein Problem und finde hier auch noch keine Antwort...der Quader an sich ist 2 schräge kästchen tief . Also muss er vom null Punkt 3 nach vorne wenn A (3/2/-1) Gegeben ist. Aber wenn das nicht Gegeben ist erkennen ich auch nicht , wie weit A nach vorne muss.
Stell die Frage noch mal anders, die erklären nur was A (3/2/-1) ist , aber nicht wie man das ohne diese Angabe ab lesen kann.
Deine (....0) kann aber nicht stimmen, dann wäre die Linie von x3 auf der kannte vom Quader (deckungsgleich) und nicht hinter ihm gestrichelt
(5....0) Kann nicht stimmen ,dann wäre die x3 ohne Berűhrung mit dem quader , sie wűrde "ûber" ihm auftauchen
Die 2 in der Mitte wűrde ich als 1.5 ablesen. ..
Stell sie noch mal ohne die Angabe (3/2/-1) auf die Antworten bin ich gespannt
Descartes wird nachgesagt, dass er eine Fliege im Raum beobachtet hat sich dabei überlegte, wie man die Position der Fliege eindeutig bestimmen kann. Dabei kam er auf die Idee, die Position der Fliege bezogen auf den Raum durch eine Längenangabe, eine Breitenangabe und eine Höhenangabe zu beschreiben. Damit waren die Grundlagen für das kartesische Koordinatensystem geschaffen.
Super, was bringt es mir? Habe geschrieben, die Grundlagen kapiere ich schon.
Das sind die Grundlagen. Es gibt bezogen auf einen Punkt (z.B. A) genau einen X1-Wert, einen X2--Wert und einen X3-Wert.
Wenn man ein dreidimensionales Koordinatensystem auf einem zweidimensionalen Blatt Papier darstellt, dann sind die Punkte leider nicht mehr eindeutig. Wenn du irgendwo einen Punkt einzeichnest, gibt es immer unendlich viele Koordinaten, die dazu passen.
Aber warum ist meine Lösung nicht richtig, ich meine es wird nicht vorgegeben, auf welcher Ebene der Punkt sich befindet, so gesehen ist (5/3/0) ja auch richtig